Wyliczenie punktu styczności w układzie współrzędnych. Kazador: Z punktu A = (6,0) poprowadzono styczne do okręgu x² + y² − 4y = 0. Oblicz pole figury ograniczonej tymi prostymi i osiami układu współrzędnych. Proszę o poradę jak obliczyć współrzędne jednego z punktów styczności (drugi z nich odnalazłem − styczna pokrywa się z osią 0X i punkt ma współrzędne (0,0) ).

Kacper: 1. równanie pęku prostych przez punkt A 2. Odległość stycznej od okręgu wynosi tyle co promień okręgu

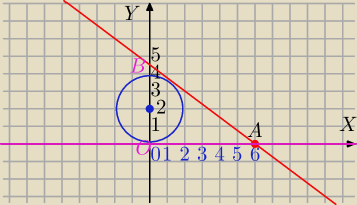
Mila: x²+(y−2)²−4=0 x²+(y−2)²=4, S=(0,2), r=2 Równanie stycznej: k: y=ax+b i A∊k⇔ 0=6a+b b=−6a y=ax−6a⇔ax−y−6a=0 Odległość stycznej od środka okręgu S=(0,2) jest równa 2.

	|a*0−2−6a|
d=		=2⇔
	√a2+1

|2+6a|=2*√a²+1 /² 32a²+24a=0 8a(4a+3)=0 a=0 to y=0 jedna styczna

	3		3
a=U{−3}[4} to y=−		x−6*(−		)⇔
	4		4

	3
y=(−		)x+4.5
	4

B=(0,4.5)

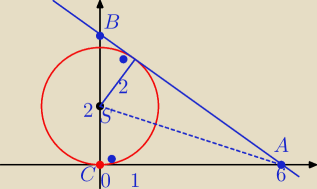
Janek191: ( x − 0)² + ( y − 2)² = 2² S = ( 0 ; 2) r = 2 pr AB ma równanie y = a x + b A = ( 6 ; 0) więc 0 = 6 a + b ⇒ b = − 6a czyli y = a x − 6 a −−−−−−−−−−−−−−−−−− a x − y − 6 a = 0 Odległość prostej AB od punktu S = ( 0 ; 2) jest równa r = 2 więc

I a*0 + 2*(−1) − 6 a I
	= 2
√a2 + 1

I − 2 − 6 a I = 2 √a² + 1 I 2 + 6 a I = 2√a² + 1 2 + 6 a = 2√a² + 1 4 + 24 a + 36 a² = 4*( a² + 1) 32 a² + 24 a = 0 8 a*( 4 a + 3) = 0

	3
a = 0 lub a = −
	4

	3		9
y = 0 lub y = −		x +		− równania stycznych do okręgu
	4		2

	9
Dla x = 0 jest y =		= 4,5
	2

więc B = ( 0; 4,5) Pole Δ ABC P = 0,5*6*4,5 = 13,5 =================