a kamczatka: Zbadaj monotoniczność i ekstrema funkcji: y = xe^1/x Dziedzina: x≠0

	1
(xe1/x)' = (x)'e1/x + (x)(e1/x)' = e1/x + xe1/x * (		)'
	x

	1		xe1/x
= e1/x + xe1/x * (−		) = e1/x −
	x2		x2

	xe1/x
= e1/x −		= 0 / *x2
	x2

= x²e^1/x − xe^1/x = 0 = x(e^1/x − e^1/x) = 0 x = 0 mi wychodzi f(x) maleje dla x∊(−∞,0) f(x) rośnie dla x∊(0,∞) a w odp mam: f(x) maleje dla x∊(0,1) f(x) rośnie dla x∊(−∞,0)∪(1,∞)

kamczatka: ? skąd ta 1 ?

john2: coś przed nawias źle wyciągnąłeś

ICSP: x²e^1/x − x*e^1/x = 0 x(x * e^1/x − e^1/x) = 0 Problemy z wyciąganiem wspólnego czynnika przed nawias ?

kamczatka: przegapiłem tego x'a , myślałem o nim ale nie wpisałem , tylko jak to teraz w nawiasie rozwiązać ? e^1/x przed nawias ?

ICSP: można

kamczatka: czyli będzie tak:? x(e^1/x(x − 1)) = 0 dzielę przez x bo x≠0 e^1/x(x − 1) = 0 więc x = 1 ?

kamczatka: i jeszcze e^1/x = 0 ale kiedy to będzie = 0 ?

john2: tak, x = 1 e^1/x nigdy nie będzie zerem

kamczatka: bo w odp mam: f(x) maleje dla x∊(0,1) f(x) rośnie dla x∊(−∞,0)∪(1,∞) i nie wiem skąd te 0

john2: z dziedziny x nie może być zerem

kamczatka: znaczy nie wiek czemu rośnie w przedziale (−∞,0) a nie tylko w (1,∞)

kamczatka: tak jakby jest dodatkowe miejsce zerowe z pochodnej x = 0, ale jak nic takiego nie ma

john2: bo nie możesz dzielić/mnożyć przez x przy nierównościach

john2: x=0 trzeba uwzględnić a właściwie "pominąć", nie może tam ani rosnąć, ani maleć, bo funkcji nie ma w tym punkcie

john2: pamiętaj, badając znak pochodnej, w zasadzie rozwiązujesz nierówności: xe^1/x(x−1)> 0 i xe^1/x(x−1)< 0 tu już nie możesz dzielić przez x, bo nie znasz znaku x

kamczatka: byś mógł to rozpisać,ten cały przykład jak się masz czas ? bo się pogubiłem

john2: ok, chwila, bo coś poszedłem za bardzo do przodu

kamczatka: ok dzięki

john2:

	e1/x(x−1)
u mnie pochodna ma postać
	x

miejsce zerowe pochodnej

e1/x(x−1)
	= 0 / *x można
x

e^1/x(x−1) = 0 / : e^1/x x−1 = 0 x =1 badamy znak pochodnej, więc pytamy, kiedy

e1/x(x−1)
	> 0 / * (x2) (znak x2 znamy)
x

xe^1/x(x−1) > 0 / e^1/x x(x−1) > 0 x∊(−∞,0)∪(1,∞) tam funkcja rośnie, bo tam jej pochodna jest dodatnia pytamy kiedy

e1/x(x−1)
	> 0
x

x(x−1) < 0 x∊ (0,1) tam maleje, bo pochodna tam < 0 jest

kamczatka: czemu taka postać pochodnej ? y = xe^1/x więc do obliczenia pochodnej korzystałem ze wzoru na mnożenie pochodnych,a tam nie ma dzielenia, skąd ten x w mianowniku u Cb

john2:

	e1/x(x−1)
tam miało być pod koniec		< 0
	x

john2:

	1
(xe1/x)' = (x)'e1/x + x*(e1/x)' = e1/x + x * e1/x * (−		) =
	x2

	1		e1/x		xe1/x		e1/x
= e1/x + e1/x * (−		) = e1/x −		=		−		=
	x		x		x		x

	xe1/x − e1/x		e1/x(x−1)
=		=
	x		x

john2:

	xe1/x
choć Twoja postać pochodnej e1/x −		jest nawet lepsza, bo
	x2

spokojnie można mnożyć prez x² przy nierówności

john2: ale nie wolno potem dzielić przez x (przy równości mogłeś, bo x ≠0)

kamczatka: jeszcze raz daje swoje rozwiązanie: y = xe^1/x Dziedzina: x ≠ 0

	1
(xe1/x)' = (x)'e1/x + (x)(e1/x)' = e1/x + xe1/x * (		)'
	x

	1		xe1/x
= e1/x + xe1/x * (−		) = e1/x −
	x2		x2

	xe1/x
= e1/x −		= 0 / *x2
	x2

= x²e^1/x − xe^1/x = 0 = x(xe^1/x − e^1/x) = 0 = x(e^1/x(x − 1)) = 0 / : x e^1/x(x − 1) = 0 x = 1 I po narysowaniu wykresu mi wychodzi: f(x) maleje dla x∊(0,1) f(x) rośnie dla x∊(1,∞) co mam zrobić aby wyszedł mi poprawny wynik, czyli taki: f(x) rośne dla x∊(−∞,0)∪(1,∞)

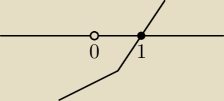
kamczatka: coś takiego mi wychodzi na wykresie

john2: tak jak mówię, nie rysuj nic, tylko rozwiąż nierówności

	xe1/x
e1/x −		> 0 /*x2
	x2

x²e^1/x − xe^1/x > 0 x(xe^1/x − e^1/x) > 0 xe^1/x(x − 1) > 0

	xe1/x
oraz e1/x −		< 0
	x2

kamczatka: a na wykresie tego nie da rady oznaczyć? czemu mi na nim nie wychodzi ?

kamczatka: nie ogarniam tego przykładu

john2: wykres działa jak masz prostą funkcję: kwadratową, albo liniową, albo inną wielomianową.

	xe1/x
Funkcji e1/x −		moim zdaniem nie narysujesz.
	x2

john2: Pamiętaj badamy znak pochodnej, pochodna to też funkcja, więc badamy znak funkcji pochodnej. Badamy znak, czyli pytamy, dla których x−ów funkcja jest nad osią x, a dla których pod nią. Można to zrobić, rozwiązując nierówność f(x) > 0 i f(x) < 0.

john2: Spróbuj w ten sposób zrobić, któryś z przykładów, który umiałeś zrobić swoim sposobem.

kamczatka: bo na e−trapezie tak tłumaczył, ze miejsca zerowe pochodnej się zaznacza na osi, potem patrząc na znak przy największym x'ie się zaczyna rysować od prawej strony góry lub dołu, i potem się oznacza − i +, gdzie − funkcja maleje,gdzie + funkcja rośnie

kamczatka: dlaczego tutaj ten sposób nie działa ?

john2: przyznam, że nie wiem, dopiero skończyłem lekcję drugą w etrapezie, zaraz spojrzę, co on robi przy tej monotoniczności.

kamczatka: ok jak będziesz wiedzieć daj znać

john2: Chyba rozumiem. Trochę dziwny ten jego sposób, On tam zaznacza, że ten sposób działa, jak mnożysz (w domyśle też dzielisz) tylko przez dodatnie liczby. Więc mając Twoją postać:

	xe1/x
f'(x) = e1/x −
	x2

Przyrównujemy do zera

	xe1/x
e1/x −		= 0 / * x2 (dodatnie, więc w porządku)
	x2

x²e^1/x − xe^1/x = 0 x(xe^1/x − e^1/x) = 0 podejrzewam, że po prostu teraz nie możesz dzielić przez x więc będziesz miał dwa "miejsca zerowe" tej funkcji pochodnej

kamczatka: a jakie to miejsca zerowe ? x = 0 i co jeszcze?

kamczatka: a możę dziedzina tego: xe^1/x to x > 0 ?

john2: nie dziedzina to x≠ 0 x(xe^1/x − e^1/x) = 0 xe^1/x(x − 1) = 0 / : e^1/x (dodatnie więc ok) x(x − 1) = 0

john2: przyznam, że niezbyt mi się podoba ten sposób, choć co ja tam wiem

kamczatka: aha dzięki,czyli źle wcześniej wyciągałem przed nawias nie to co trzeba

john2: w zasadzie bardziej chodzi o ten drugi błąd o 18:18, gdzie podzieliłeś przez x (to wcale nie jest błąd, bo x ≠0, ale robiąc sposobem Krystiana to chyba jest błąd, bo x jest niewiadomego znaku)

kamczatka: 40 kilka postów ten temat miał heh