Rozwiąż nierówność
Mati: Rozwiąż nierówność ||x+1|−2|<4. Oblicz sumę wszystkich liczb całkowitych należących do zbioru
rozwiązań tej nierówności.
||x+1|−2|<4 <=> |x+1|<6 i |x+1|>−2
1. |x+1| < 6 <=> x+1<6 i x+1>−6
x<5 x>−7
x ∊ (−7,5)
2. |x+1|>−2 <=> x+1>−2 lub x+1<2
x>−3 x<1
nie wiem jak ten przedział tu będzie wyglądać...
proszę o pomoc w dokończeniu zadania...
16 wrz 18:20
Kacper:
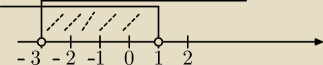
16 wrz 18:30
Mati: x ∊ (−3,1) dziękuję

ale nie jestem pewny co mam teraz dalej zrobić...połączyć te dwa
rozwiązania w jaki sposób?
16 wrz 18:34
PW: Mati, robisz podstawowy (niestety bardzo popularny) błąd.
To nie jest prawda, że (cytuję)
2. |x+1|>−2 <=> x+1>−2 lub x+1<2.
Jest oczywiste, że zdanie |u| > −2 jest prawdziwe dla każdej u − nie trzeba tu nic rozwiązywać,
zastosować definicję wartości bezwzględnej (jest nieujemna).
16 wrz 18:42
Mati: ale co tutaj jest błędem bo nie rozumiem?

16 wrz 18:53
Kacper: O

nie czytałem

|x|≥0 zawsze, czyli |x|>−2
16 wrz 18:56
PW: Przeczytaj jeszcze raz. Jest idiotyczne zastanawianie się, dla jakich x
|x+1| > −2,
bo taka nierówność jest prawdziwa dla wszystkich x. A co wyliczyłeś swoją (błędną) metodą?
16 wrz 18:58
Mati: No tak, racja

czyli ogólnie jak to powinienem zapisać?

16 wrz 19:01
Mati: |x+1|>−2 <=> x>−3?
16 wrz 19:08
Mati: czy w ogóle tego nie rozpatrywać?
16 wrz 19:09
PW: Zaproponuję Ci sposób rozwiązania inny, prosty i pozbawiiony takich niebezpieczeństw.
W zadaniu pytają o liczby całkowite x spełniające nierówność. Skoro całkowite, to lewa strona
nierówności jest liczbą naturalną lub zerem. Ile jest takich liczb mniejszych od 4? Ramtem
cztery: 0, 1, 2 i 3.
Rozwiązujemy w zbiorze liczb całkowitych równości:
||x+1|−2| = 0 lub ||x+1|−2| = 1 lub ||x+1|−2|=2 lub ||x+1|−2| = 3.
Rozwiązania tych równości są zbiorem szukanych liczb, których suma jest odpowiedzią.
16 wrz 19:23

 ale nie jestem pewny co mam teraz dalej zrobić...połączyć te dwa
rozwiązania w jaki sposób?
ale nie jestem pewny co mam teraz dalej zrobić...połączyć te dwa
rozwiązania w jaki sposób?

 nie czytałem
nie czytałem  |x|≥0 zawsze, czyli |x|>−2
|x|≥0 zawsze, czyli |x|>−2
 czyli ogólnie jak to powinienem zapisać?
czyli ogólnie jak to powinienem zapisać? 