prawdopodobieństwo wiktoria: cześć czy może ktos spr czy dobrze rozwiązałam zadanie z odcinak (−1,4) losuję dwie liczby.NIech A−zdarzenie polegające na wylosowaniu dwóch liczb dodatnich, B−zdarzenie polegające na tym, że droga z losowanych liczb jest ujemna,, C zdarzenie polegające na tym ze pierwsza z wylosowanyc liczb jest dodatnia. a) zbadaj niezaleznosc zdarzeń A i B b)zbadaj niezależność zdarzeń A i C c)policz P(A/C) d)policz P(B/C) λ(Ω)=25 16 P(A)= 25 5 P(B)= 25 20 P(C)= 25 a) P(A∩B)=P(A)*P(B) (A∩B)=Φ P(Φ)=0 16 5 P(A)*P(B)= * P(A∩B)≠P(A)*P(B) 25 25 b)P(C∩B)=P(C)*P(B) 5 (C∩B)={ (−1,4)}=5 P(C∩B)= − czy to tak powinno byc? 25 bo pkt a wydaje mi sie ze chyba powinien byc tak rozwiazany a z tym to troce strzelanie a niezrozumienie tego zatrzymuje mnie w rozwiazaniu c i d

Maslanek: Losujemy tylko liczby całkowite?

Janek191: Dowolne dwie liczby rzeczywiste należące do ( − 1 ; 4 )

Maslanek: Rozwiązanie wydaje się wskazywać na zupełnie co innego

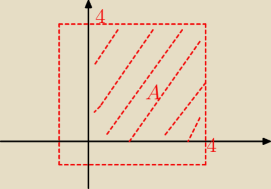
Janek191: Rysunek do zdarzenia A I Ω I = 5*5 = 25 I A I = 4*4 = 16

	16
P( A ) =
	25

Janek191:

	5*1		5
P( B) =		=
	25		25

	4*5		20
P( C ) =		=
	25		25

ok

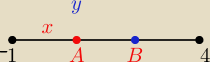
Maslanek: Rozważmy najpierw przestrzeń prawdopodobieństwa: Ω={(x,y): −1<x<4 oraz −1<y<4} Teraz zdarzenie sprzyjające: A={(x,y): 0<x<4 oraz 0<y<4} B={(x,y): −1<x<4 oraz −1<y<0} C={(x,y): 0<x<4 oraz −1<y<4} a) Zdarzenia są niezalezne jeśli P(A∩B)=P(A)*P(B) b) patrz wyżej c) A\C=∅ d) B\C={(x,y): −1<x≤0 oraz −1<y<0}

Janek191: P( A ∩ B) = 0

	16		5		80
P( A) *P( B) =		*		=		= 0,128
	25		25		625

więc P( A ∩ B ) ≠ P( A) * P( B)

wiktoria: dlaczego w podpunkcie c wyszło Ci ze jest zbiorem pustym bo nie rozumiem bo ja sobie to tłumacze tak(oczywiscie nie wiem czy dobrze) P(A/C)−zdarzenie polegajace na wylosowaniu dwoch liczb dodatnich pod warunkiem ze pierwsza jest dodatnia

	16
A ∩ C=(0,4)x(0,4)=16 P(A ∩ C)=
	25

Maslanek: To proszę Pani stosujemy poprawny zapis P(A\C) − prawdopodobieństwo różnicy zbiorów A i C P(A|C) − prawdopodobieństwo A przy warunku C Rozumiem, że jest pani na studiach, bo prawdopodobieństwa geometrycznego w szkole średniej nie ma. I to pewnie na jakimś kierunku związanym z matematyką. Wyrażajmy się więc precyzyjnie