---- Kinga: Witam. Czy pomoże ktoś w 3 zadaniach? Przy okazji tłumacząc po trochu o co chodzi? Będę wdzięczna za rysunki. 1. W ostrosłupie prawidłowym czworokątnym zaznacz: a) kąt dwuścienny, który wyznacza ściana boczna z podstawą b) kąt dwuścienny między sąsiednimi ścianami bocznymi 2. Punkty M i N leżą na jednej ścianie kąta dwuściennego i są oddalone od jego krawędzi odpowiednio o 24 cm i 40 cm. Odległość punktu N od płaszczyzny drugiej ściany tego kąta dwuściennego jest równa 15 cm. Oblicz odległość punktu M od tej płaszczyzny. 3. Podstawą ostrosłupa prawidłowego jest trójkąt równoboczny o krawędzi 5 cm. Oblicz tangens kąta dwuściennego między ścianą boczną i podstawą ostrosłupa, wiedząc, że wysokość ostrosłupa jest równa 15 cm.

daras: https://matematykaszkolna.pl/forum/257934.html

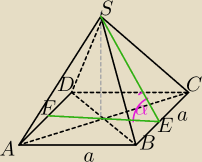
Mila: 1) a α=∡FES−kąt między ściana boczną a podstawą ostrosłupa

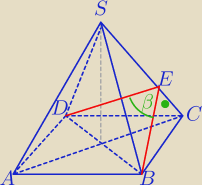
Mila: 1)b β− kąt między sąsiednimi ścianami bocznymi BE ⊥SC i DE ⊥ SC

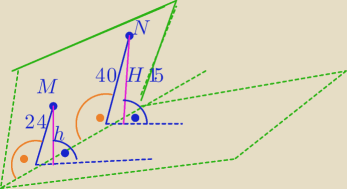
Mila: Otwórz książkę leżącą na stole w taki sposób, aby był kąt ostry między częścią górną i dolną, zaznacz dwa punkty i rzutuj na dolną część, to zrozumiesz. 2) Z podobieństwa trójkątów :

24		40
	=
h		15

h=9 cm ====

Mila: 3) rozwiąż sama, bo teorię masz wyjaśnioną.