Planimetria - trapez Jacek: Oblicz długość odcinka (równoległego do podstawy) dzielącego trapez o podstawach 8 i 4, na dwa trapezy o jednakowych polach.

pigor: ..., niech x= ? − szukana długość odcinka, to z podobieństwa trapezu górnego do całego w skali k= ^x₈ i równości pól podziału tym odcinkiem danego trapezu mamy równanie: ¹₂=k² ⇔ ¹₂=(^x₈)² ⇔ x²=32 ⇒ x=4√2 ≈ 5.66 . ...

Mila: pigor, trapezy nie są podobne. Popraw. x=2√10

Jacek: jak to obliczyłeś/aś?

pigor: ... , dzięki Mila przepraszam, za moją ... niemoc umysłową; to może tak : (^x−4₄)²= ¹₂ i x>4 ⇒ (x−4)²= 8 ⇒ |x−4|= 2√2 ⇒ ⇒ x−4= 2√2 ⇒ x=4+2√2 ⇔ x=2(2+√2) ≈ 6,82. ...

Mila:

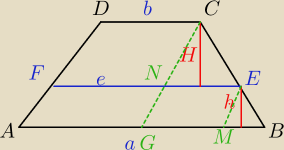
	√a2+b2
Można skorzystać z gotowego wzoru: e=		srednia kwadratowa.
	√2

Wyprowadzamy tak: Oznaczenie : |EF|=e, CG||AD, EM||AD

1		1
	(a+e)*h=		*(e+b)*H z treści zadania ⇔
2		2

(a+e)*h=(e+b)*H ⇔

a+e		H
	=
e+b		h

	H		NE		e−b
ΔNEC∼ΔMBE⇔		=		=		⇔
	h		MB		a−e

a+e		e−b
	=		⇔
e+b		a−e

a²−e²=e²−b² a²+b²=2e²

	a2+b2
e2=
	2

	√a2+b2
e=		srednia kwadratowa.
	√2

e=√(8²+4²)/2=√(64+16):2=√40 e=2√10 ==========