prawdopodobienstwo zadanie: Oblicz prawdopodobienstwo wybrania przedmiotu I gatunku, jesli jest 5% brakow, a 20% przedmiotow dobrych jest II gatunku. Moge poprosic o pomoc? Jak rozpoznac czy chodzi o prawdopodobienstwo warunkowe albo o niezaleznosc zdarzen?

zadanie: ?

pigor: hmm..., dla mnie p=75%= 0,75 to szukane prawdopodobieństwo przy jednokrotnym losowaniu i przy tak sformułowanym zadaniu i nie potrzebna tu wiedza o niczym więcej tylko definicja klasyczna prawdopodobieństwa i tyle ...

zadanie: odp. 0.76. Jest to zadanie z dzialu prawdopodobienstwa calkowitego oraz wzor Bayesa.

PW: Przedmioty dobre stanowią 95% całości próby. W tych 95% jest 20% przedmiotów II gatunku, czyli 19% całości (0,95·020 = 0,19). Mamy więc: 5% braków, 19% przedmiotów II gatunku i 76% przedmiotów I gatunku. Jeżeli koniecznie prawdopodobieństwo całkowite, to: C − przedmioty dobre B − braki D − przedmioty II gatunku. P(C) = P(B') = P(Ω)−P(B) = 1−0,05 = 0,95 P(D|C) = 0,20 Zgodnie z definicją

	P(D∩C)
P((D|C) =		,
	P(C)

a ponieważ D∩C = D

	P(D)
P((D|C) =		,
	P(C)

P(D) = P(D|C)·P(C) P(D) = 0,20·0,95 = 0,19 D⊂C, zatem P(C\D) = P(C) − P(D) = 0,95 − 0,19 = 0,76 − to jest odpowiedź, gdyż przedmioty I gatunku to właśnie C\D. Tak jak pisał pigor, stosowanie tutaj tej "teorii' jest zbędne. Pewnie mu się wcisnął sąsiedni klawisz, dlatego ma 0,75

pigor: ..., przyznaję, że moje rozumowanie było jednak ... złe; pozdrawiam

PW: Tego nie wiedzieliśmy, bo go nie przedstawiłeś

Mila: 0,8*0,95=0,76 liczyłam z drzewka.

zadanie: dziekuje a jakby wygladalo drzewko do tego zadania?

Mila: Jutro narysuję. Dzisiaj. Dobranoc

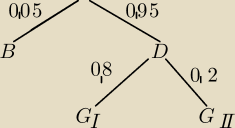
Mila: P(G_I)=0,95*0,8=0,76

zadanie: dziekuje

Mila: Już po sesji?

zadanie: tak

Mila: Gratulacje. Teraz odpoczywaj.