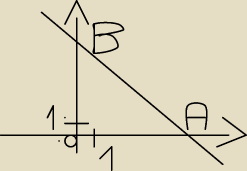 Prosta o równaniu y=6−2x wraz z osiami układu współrzędnych wyznacza trójkąt ABO. W trójkąt ten
wpisano prostokąt w ten sposob, że jeden z wierzchołków prostokąta znajduje się w początku
układu współrzędnych, a dwa inne na osiach układu współrzędnych. Czwarty wierzchoółek leży na
odcinu AB. Uzasadnij, że pole tego prosokąta nie jest większe od połowy pola trójkąta ABO.
Prosta o równaniu y=6−2x wraz z osiami układu współrzędnych wyznacza trójkąt ABO. W trójkąt ten
wpisano prostokąt w ten sposob, że jeden z wierzchołków prostokąta znajduje się w początku
układu współrzędnych, a dwa inne na osiach układu współrzędnych. Czwarty wierzchoółek leży na
odcinu AB. Uzasadnij, że pole tego prosokąta nie jest większe od połowy pola trójkąta ABO.
 dla x1 y1=−2x1+6
S▭=x1(−2x1+6)
S▭=−2x12+6x1
Smax▭ dla x1w
x1w=1,5
zatem Smax▭=−4,5+9=4,5
gdy S{△ABO}=9
dla x1 y1=−2x1+6
S▭=x1(−2x1+6)
S▭=−2x12+6x1
Smax▭ dla x1w
x1w=1,5
zatem Smax▭=−4,5+9=4,5
gdy S{△ABO}=9

| x | y | ||
+ | =1 | ||
| 3 | 6 |