Mam problem z zadaniem z kombinatoryki. New Order: Przy okrągłym stole, którego miejsca są nierozróżnialne, ma usiąść 5 kobiet i 5 mężczyzn. Na ile sposobów można posadzić te osoby tak, aby każda kobieta miała za sąsiadów dwóch mężczyzn?

PW: Miejsca są „nierozróżnialne”, czy „równorzędne”?

New Order: nierozróżnialne

wmboczek: muszą siedzieć naprzemian 5! możliwości kobiet 5! panów podzielić na 10 bo okrągły stół

New Order: to niestety nie dało odpowiedzi na pytanie

PW: Ja rozumiem, że można 10 nierozróżnialnych piłeczek rozmieścić w 3 szufladach (rozróżnialnych lub nie). Gdyby miejsca przy stole były nierozróżnialne, to jakim cudem usadzić tych ludzi − wskazać cioci nierozróżnialne miejsce? Pozdrowienia dla autora zadania. Od takich zaczynają się kłopoty z kombinatoryką.

bezendu: Źle wmboczek

5!*5!
5

Miejsca przy stole nie są rozróżnialne, więc liczbę przypadków dzielimy przez 5 a nie przez 10

New Order: Tak to czasem bywa z tymi zadaniami.

New Order: I chyba odpowiedź 2880 jest dobra

New Order: Dzięki!

New Order: Ale jak to nazwać?

bezendu: Kombinatoryka, reguła mnożenia.

Trivial: Nierozróżnialne miejsca przy stole. A to ci dopiero!

New Order: rozumiem

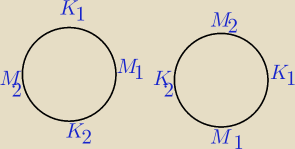
Mila: Chodzi chyba o to, że układy ( dla 4 osób) −np. takie jak na rysunku uznaje się za jednakowe.

Kacper: Jeśli osoby mają tych samych sąsiadów, to ustawienie jest jednakowe.

bezendu: Jaka jest odpowiedź w zbiorze ?

Trivial: bezendu, chcesz zrewersować myśli autora z odpowiedzi?

bezendu: Nie Tylko pytałem jak jest prawidłowa odpowiedź. Teraz to ja zabieram się za programowanie.

PW: bezencu, i Ty też opowiadasz o nierozróżnialnych miejscach? Wyjaśnijmy pewną terminologię. Żeby usadzić ludzi przy stole, czyli ustanowić dla każdego z nich przyporządkowanie różnowartościowe człowiek → miejsce przy stole, to miejsca muszą być rozróżnialne, ponumerowane kolejno np. przeciwnie do ruchu wskazówek zegara. Funkcji takiej nie trzeba zapisywać "na okrągło", nie ma takiego pojęcia matematycznego. Usadzenie ludzi przy stole to utworzenie permutacji, np. (k₁,k₂,...,k₅, m₁,m₂,...,m₅) → (3,1,2,5,10,6,8,7,4,9) − widać jak siedzą? k₂ i k₅ są sąsiadkami, bo zajmują miejsca 1. i 10. Przy okrągłym stole, przy którym miejsca traktuje się jako równorzędne ważne jest w jakiej kolejności ludzie siedzą (kto ma jakiego sąsiada z prawej i lewej strony), a nie na którym krześle. Permutacje, w których wszystkie wartości są przesunięte o 1, 2, 3, ..., traktuje się jako równorzędne, np. równorzędne są permutacje (3,1,2,5,10,6,8,7,4,9) i (4,2,3,6,1,7,9,8.5,10). Każdy usiadł na miejscu o numerze o 1 większym, czyli przesunęli się wszyscy "o jedno miejsce przeciwnie do ruchu wskazówek zegara", ale sąsiedzi zostali tacy sami, teraz np. panie k₂ i k₅ zajmują miejsca 2. i 1. Dla formalności trzeba dodać, że dodawanie numerów miejsc traktujemy "modulo 10", czyli 10+1 = 1.