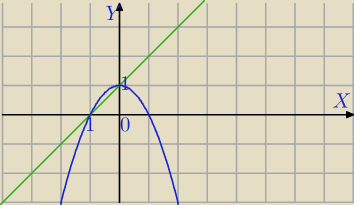
całka podwójna asd: Całka podwójna ∫∫(2x³+4y)dxdy ograniczona krzywymi y=x+1, y=−x²+1 Narysowałem, te krzywe, wiem ze punkt przecięcia będzie dla −1≤x≤0, a nie mam pojęcia jak sprawa będzie wyglądała dla y ?

Krzysiek: http://www.wolframalpha.com/input/?t=crmtb01&f=ob&i=y%3Dx%2B1%2C%20y%3D1-x%5E2 granice całkowania dla 'y' to [x+1,1−x²]

MQ: To jest całka iterowana. Najpierw całkujesz po y w ganicach od y=x+1 do y=−x²+1, a potem po x w granicach takich jakie podałeś.

Mila: −1≤x≤0 x+1≤y≤−x²+1

asd: Rozumiem, ze dla y, x+1 ogranicza z dołu, a −x²+1 z góry ?

Mila: Tak.

asd:

	1
Niestety wynik powinien wyjść		, a ja dostaje zupełnie coś innego. O to moje obliczenia:
	3

Policzyłem całkę nieoznaczoną po y: ∫(2x³+4y)dy=∫2x³dy+∫4ydy=2x³y+2y² całka oznaczona: 1−x² [2x³+2y²]| = [2x³−2x⁵+4x⁴−4x²]−[2x⁴+2x³+2x²+4x+2]=−2x⁵+2x⁴−6x²−4x−2 x+1 Proszę o sprawdzenie tego fragmentu zadania, czy do tego momentu jest dobrze ?

Krzysiek: wolfram mówi,że źle http://www.wolframalpha.com/input/?i=integrate_%281%2Bx%29%5E%281-x%5E2%29+%282x%5E3%2B4y%29dy

asd: No tak, ale to mi nic nie daje, bo nei wiem gdzie jest błąd

Krzysiek: 2x³(1−x²)+2(1−x²)²−[2x³(1+x)+2(1+x)²]= 2x³−2x⁵+2−4x²+2x⁴−2x³−2x⁴−2−4x−2x²= =−2x⁵−6x²−4x

asd: Nie kumam, tego działania 2(1−x²)² tutaj trzeba skorzystać ze wzoru skróconego mnożenia ?

asd: up

Mila: jeśli y=x+1 to y²=(x+1)²=x²+2x+1 jeśli y=(1−x²) to y²=(1−x²)²=1−2x²+x⁴

asd: Dzięki wielkie

Mila: