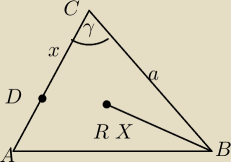
 Mam takie zadanko z planimetrii: W trójkącie ABC bok BC ma długość a, a kąt ACB ma miarę γ.
Punkt D∊AC i |DC|= x. Oblicz lim R(x), gdzie R(x) jest promieniem okręgu opisanego na ΔBCD
. x→0
Mam takie zadanko z planimetrii: W trójkącie ABC bok BC ma długość a, a kąt ACB ma miarę γ.
Punkt D∊AC i |DC|= x. Oblicz lim R(x), gdzie R(x) jest promieniem okręgu opisanego na ΔBCD
. x→0







| |DB| | √a2+x2−2axcosγ | |||
R(x)= | = | ⇒ limx→0 R{x}= | ||
| 2sinγ | sinγ |
| √a2+x2−2axcosγ | a | |||
= limx→0 | = | ... i to tyle ...  | ||
| sinγ | sinγ |