Równanie okręgu Jacek: Napisz równanie stycznych do okręgu x²+y²+12x−2y+17=0 i równoległych do prostej 2x+y−5=0 Mógłby mi ktoś pokazać na tym przykładzie jak rozwiązywać takiego typu zadania? Za udzieloną pomoc bardzo dziękuję

Kacper: Zrób rysunka na początek

Jacek: Ale po co rysunek tutaj na pewno trzeba skorzystać z warunku równoległości prostych i jakiejś dodatkowej zależności/ wzoru

Kacper: To bez rysunku ja ci nie pomogę, bo w geometrii rysunek to podstawa i z niego widać co można wykorzystać.

Jacek: to już rysuję daj mi chwilkę

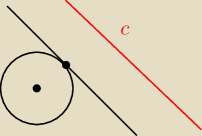
Jacek: czerwonym kolorem oznaczona jest prosta o równaniu 2x+y+5=0 czarnym natomiast prosta o styczna do okręgu o równaniu x²+y²+12x−2y+17=0

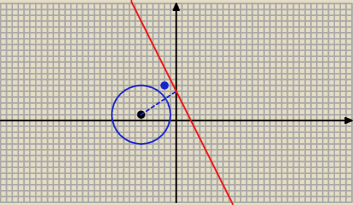
Janek191: x² + y² + 12 x − 2 y + 17 = 0 ( x + 6)² − 36 + ( y − 1)² − 1 + 17 = 0 ( x + 6)² + ( y − 1)² = 20 = (2√5)² S = ( − 6; 1) r = 2√5 oraz 2 x + y − 5 = 0 ⇒ y = − 2 x + 5 Prosta równoległa do danej ma równanie : y = − 2 x + b lub 2 x + y − b = 0 Odległość tej prostej od punktu S = ( − 6; 1) jest równa 2√5 Skorzystaj z odpowiedniego wzoru i dokończ

Jacek: nie wiem dokładnie z którego czy to ten

IAx+By+CI
√A2+B2

Kacper:

Jacek:

2*(−6)+1−5		I−12+1−5I		16
	=		=
√22+12		√5		√5

Kacper: A co zrobiłeś z niewiadomą b?

Jacek: Dobrze jest rozwiązane i czy to koniec zadania Kacprze?

Jacek: 2 x + y − 5 = 0 wziąłem pod uwagę to równanie

Jacek:

11−b
√5

Janek191: Prosta o równaniu 2 x + y − b = 0 ma być styczna do danego okręgu !

Jacek: nie rozumiem za bardzo o co chodzi i z czego mam skorzystać

Janek191:

I 2*( −6) + 1*1 − b I
	= 2√5 / * √5
√22 + 12

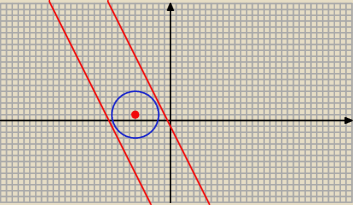
I − 12 + 1 − b I = 10 I − 11 − b I = 10 I 11 + b I = 10 11 + b = − 10 lub 11 + b = 10 b = − 21 lub b = − 1 Równania prostych stycznych: 2 x + y + 21 = 0 i 2 x + y + 1 = 0 =======================================

Jacek: Czasami się zastanawiam jak wy widzicie te liczby bo ja mam z tym problem żeby to w taki sposób jak wy to zobaczyć

Jacek: Tutaj sposób rozwiązywania jest taki sam czy się zmienia : Napisać równania stycznych do okręgu x²+y²−2x+6y+5=0 i prostopadłych do prostej x−2y=0 Rozpisałem sobie to tak jak na poście z 14:29 i mam taką postać (x−1)²+(y+3)²=√15² r=√15

Kacper: Zmieniają się tylko dane

Janek191: Napisz równanie dowolnej prostej prostopadłej do danej prostej i dalej tak jak w poprzednim zadaniu

Janek191: Równanie okręgu − źle ! Powinno być ( x − 1)² + ( y + 3)² = 5 r = √5

Kacper: Ja nawet tego nie sprawdzałem

Janek191:

	1
x − 2y = 0 ⇒ 2y = x ⇒ y =		x
	2

Prosta prostopadła ma równanie y = − 2 x + b

Janek191: Na wszelki wypadek należy sprawdzić

Jacek: Czyli tak S(1;−3) x−2y−b=0 równanie prostej prostopadłej do prostej x−2y=0

1*1−2*(−3)−b
	=√15
√12+22

1+6−b
	=√15
√5

dobrze zacząłem?

Jacek: skąd liczycie tą prostą prostopadłą

Jacek: a₁a₂=−1 tak? Ale skąd ta 2

Janek191: Podałem wyżej równanie prostej prostopadłej do danej prostej : y = − 2 x + b lub w postaci ogólnej 2 x + y − b = 0

Janek191:

1
	*( −2) = − 1
2

Janek191: Tam jest r = √5 !

Janek191: S = ( 1 ; − 3) r = √5 2 x + y − b = 0 i liczymy odległość tej prostej od S. Ta odległość musi być równa √5

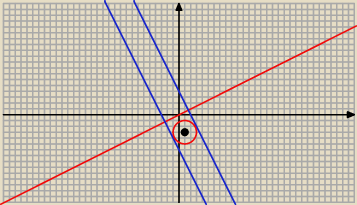
Jacek: już wyliczone panowie 2x+y+6=0 i 2x+y−4=0 Jakby popatrzeć na ten schemat działania to nie jest to takie trudne tylko potrzeba wprawy

Janek191:

Janek191: Jest ok