geometria
tyu:
witam wszystkich
Mam takie zadanie
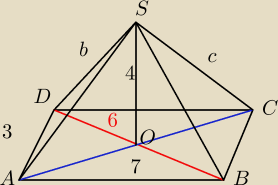
"Podstawą ostrosłupa jest równoległobok o bokach długości 3cm i 7 cm którego jedna z
przekątnych ma 6 cm długości. Spodkiem wysokości ostrosłupa jest punkt przecięcia przekątnych
podstawy. Wysokość ostrosłupa ma długość 4 cm. Oblicz długość krawędzi bocznych ostrosłupa. "
tutaj
http://www.matematyka.pl/157204.htm jest podpowiedź do rozwiązania, ale tw cosinusów stosuje się − o ile się nie mylę −
jeśli wiemy, że jest jeden kąt prosty. A tutaj tego nie wiemy, który kąt jest prosty. Nie wiem
jak kąt obliczyć za pomocą tego tw. cosinusów.
Wiem, że krawędź boczna b ma długość 5, bo DO= 0,5*6=3 I wtedy jest trójkąt o bokach 3,4,5.
13 wrz 11:10
tyu: rozwiązałem inaczej
13 wrz 11:18
Saizou :
jeśli jeden kąt jest prosty to stosujemy tw. Pitagorasa, możesz też stosować tw. cosinusów
(zwane też uogólnionym tw. Pitagorasa, bo dla α=90
o uzyskamy tw. Pitagorasa
∠BAD=x zatem ∠ADB=180−x
z tw. cosinusów mamy że
6
2=3
2+7
2−2•3•7cosx
36=9+49−42cosx
−22=−42cosx
a cos(180−x)=−cosx
13 wrz 11:21
tyu: dziękuję za pomoc.
13 wrz 11:34
tyu:
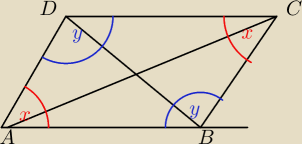
mam pytanie czy tutaj przez
Saizou jest poprawnie obliczone, ze ∠ADB=180−x
bo chyb powinno być ∠AD
C=180−x
jeśli suma kątów wewnętrznych to 360
2y=360−2x
y=180− x oraz y=I<AD
CI
13 wrz 12:04
Bogdan:
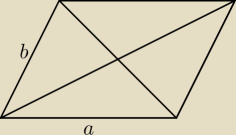
e, f − długości przekątnych.
Przyda się zależność: e
2 + f
2 = 2a
2 + 2b
2
13 wrz 12:29
Saizou : oczywiście ADC=180−x
13 wrz 12:35
Saizou :
to niech tyu to wykaże co Bogdan napisał
13 wrz 12:36
tyu: dziękuję. Ja właśnie obliczyłem tym sposobem co Bogdan napisał. Kiedyś go zapisałem sobie
przy innym zadaniu, w którym właśnie Bogdan podał ten wzór. Tylko że jak są dwa sposoby,
to dobrze jest umieć dwa, bo czasem jeden sposób w stresie można zapomnieć
13 wrz 12:41
Piotr 10: Udowodnij to teraz ( dowód bardzo prosty i krótki )
13 wrz 12:42
tyu: okej
13 wrz 12:44
tyu: ja pokaże swoje obliczenia do zadania, bo dowodu tego twierdzenia nie mam
e2+62=2(72+32)
e2+36=2(49+9)
e2=60
e=4√5
IASI=√ (2√5)2 + 42 = √ 20 + 16 = √ 36 = 6
13 wrz 12:50
Piotr 10:
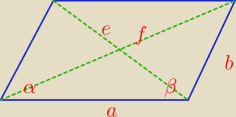
f
2 = a
2+b
2 −2ab*cosβ
e
2 = a
2+b
2 − 2ab*cosα
β = 180
0 − α
f
2 = a
2+b
2 +2ab*cosα
e
2 = a
2+b
2 − 2ab*cosα
Dodając stronami otrzymuje,że:
e
2+f
2 = 2(a
2+b
2).
13 wrz 12:53
Saizou :
to się pogłów nad dowodem, bo inaczej to bez sensu podstawić i gotowe xd
13 wrz 12:54
tyu: 
przepisuję sobie dowód do kajetu
dzięki wszystkim
13 wrz 12:55
tyu: w moim poście z 12:50 jest omyłka
powinno być e2=80
13 wrz 13:23