. Piotr 10: Witam, mam pytanie Czy zawsze da narysować się dwie wspólne styczne dla dwóch okręgów o różnych promieniach ? Bo rysuje sobie konstrukcyjnie i nie wyszło mi za drugim razem.

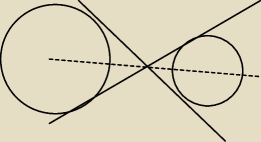
Kacper: Zależy od położenia okręgów Na rysunku powyżej − brak wspólnych stycznych

Piotr 10: Ale mi chodzi o przypadek, gdy okręgi są rozłączne zewnętrznie

Piotr 10: Mi z rysunków wychodzi, że nie zawsze. Ale nie wiem czy ja źle coś robię czy nie

PW: Wtedy tak. Okręgi są jednokładne, stosunek jednokładności jest dodatni lub ujemny, zależnie od położenia wspólnego punktu stycznych.

Kacper: To zaraz rysuję Coś takiego

Kacper: Pokaż rysunek, gdzie nie dajesz rady narysować

Piotr 10: Robiłem za pomocą tej metody http://matinfa.pl/niezbednik/styczne-do-dwoch-okregow/ I za pierwszym razem wyszło, a teraz za 2 i 3 razem nie wyszło.

Piotr 10: Czy okrąg o kolorze niebieskim i okrąg o kolorze pomarańczowym mają mieć takie same promienie ?

Kacper: Ciekawa konstrukcja Nadal nie wiem dlaczego ci się nie udało

Piotr 10: Chyba już wiem gdzie mam błąd zaraz wrócę ide cos zrobic

Kacper: Oczywiście, że nie są takie same

Piotr 10: Problem rozwiązany . Źle zinterpretowałem tekst

Kacper: Promień pomarańczowego to R−r (duży odjąć mały)

PW: Piotrze, nie ucz się z takich horendalnych kącików internetowych. Podany tam sposób konstrukcji brzmi jak przepis na pieczenie ciasta. !. Weź to 2. Zrób tamto itd. Jeżeli w punkcie 1. czytam (cytuję): Zmniejszamy promień obu okręgów o promień mniejszego okręgu, to w tym momencie wyłączam komputer.

Piotr 10: A wcześniej rysowałem, żę promień p. = promień n. mały

Kacper: PW umiesz piec ciasta? Bo ja nie mam piekarnika, a chętnie zjadłbym jakieś

Piotr 10: PW po prostu było mi potrzebne zrobić to konstrukcyjnie . A ten sposób jest ciekawy dla mnie

PW: Jeżeli tylko rozumiesz dlaczego taka konstrukcja jest poprawna. to dobrze.

Saizou : Cześć Kacper, na pewno coś znajdziesz http://kotlet.tv/przepisy/bez-pieczenia/

Kacper: Cześć Saizou Wszystko ładnie wygląda, ale nie wiem czy mam aż taki talent Tak jak powiedział PW ważne, żeby wiedzieć dlaczego dana konstrukcja jest prawdziwa. Zadanie dla Piotrka to uzasadnić prawdziwość podanej konstrukcji

Piotr 10: Spoko, uzasadnię później

Mila: Narysowałeś?

Piotr 10: Mila tak narysowałem