Zilustruj zbiór wszystkich punktów płaszczyzny, których współrzędne (x,y) spełni asdf: 2|x|−|y+2|=1 mógłby mi ktoś wytłumaczyć jak to się robi?

Kacper: rozpatrz przypadki: x≥0 i y≥0 x≥0 i y<0 x<0 i y≥0 x<0 i y<0

J: .... wszędzie zamiast y , ma być: y + 2

Kacper: tak oczywiście

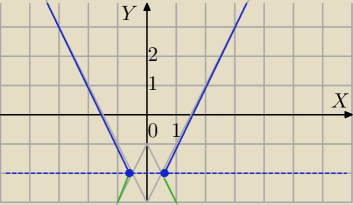
Mila: 2|x|=|y+2|+1 1) y+2≥0⇔y≥−2 ( punkty nad prosta y=−2) i mamy równanie: y+2+1=2|x| y=2|x|−3 2) y+2<0⇔y<−2 wtedy masz równanie: 2|x|=−y−2+1⇔ y=−2|x|−1

asdf: jedno pytanie pewnie uznacie ze głupie ale nie mam rozszerzonej majcy w szkole więc czemu y=2|x|−3 jest malejąca? a y=−2|x|−1 jest rosnaca?

asdf: ok juz wykombinowałem

asdf: a jeszcze 1 mam takie cos |x−4|+|3y|=6 i robie: 3y≥0 ⇔ y≥0(wiec punkty nad prostą y=0) 3y−6=|x−4|

	|x−4|
y=		+2
	3

i jezeli 3y<0 ⇔ y<0

	|x−4|
−3y=6−
	3

i wychodzi mi jakiś dziwny wykres (inny od tego na koncu ksiazki)

Kacper: Skoro nie masz matematyki to dlaczego robisz takie zadania? Chcesz rozszerzenie zdawać?

asdf: tak bo potrzebuje do studiów a w liceum niemam jej rozszerzonej wiec staram się sam nauczyć z wasza pomocą

Kacper: dla y≥0 mamy

	|x−4|
|x−4|+3y=6 ⇒y=2−
	3

asdf: I tak sie zastanawiam teraz jakby te proste załamywały sie w (4,0) zamiast w y=0 i patrząc od prawej to by było dobrze

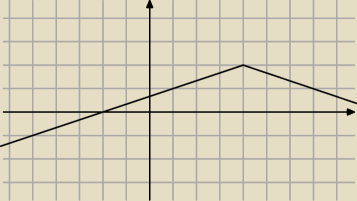
Kacper: Wykres tego co powyżej pisałem

Kacper: Oczywiście wybieramy tylko fragment dla y≥0

asdf: dzieki chyba w koncu zrozumialem jak sie rysuje te wykresy

Kacper: