Stereometria sześcian Kxi: W sześcianie ABCDA'B'C'D' o krawędzi długości a końce przekątnej dolnej podstawy BD połączono z punktem P na nierównoległej przekątnej górnej podstawy. Otrzymany trójkąt ma pole równe

	3
		a2 . Wyznacz sinus kąta nachylenia tego trójkąta do dolnej podstawy sześcianu oraz
	4

pole przekroju do którego należy przekątna BD i punkt P.

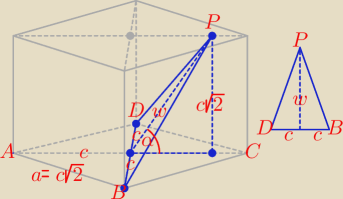Bogdan: Pierwsza część zadania:

	3		3		c√2
a2 = 2c2, c*w =		*2c2 ⇒ w =		c i sinα =		=
	4		2		3   c 2

...

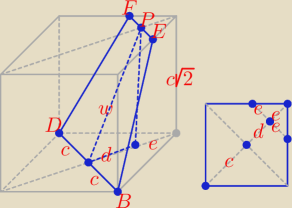Bogdan: Druga część zadania:

	9		1		1
d2 = w2 − 2c2 =		c2 − 2c2 =		c2 ⇒ d =		c i d = c − e ⇒ e = ...
	4		4		2

	1
Pole przekroju DBEF (trapez) =		*w*(2c + 2e) = ...
	2