Trygonometria. romb James: Przekątne rombu mają długości 4 i 2√5. Oblicz tg α + 9 cos α, gdzie α jest miarą kąta ostrego tego rombu.

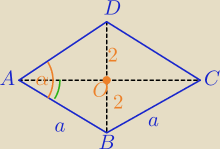
Mila: |OC|=√5=|AO| |OB|=2 Przekątne są dwusiecznymi kątów wewnętrznych a²=2²+(√5)² a²=9 a=3 WΔAOB:

	α		2
sin		=
	2		3

	α		√5
cos		=
	2		3

	α		α		2		√5
sinα=2*sin		*cos		=2*		*
	2		2		3		3

	4√5
sinα=
	9

sin²α+cos²α=1

	4√5
(		)2+cos2α=1
	9

	80		1
cos2α=1−		=
	81		81

	1
cosα=
	9

	sinα
tgα=
	cosα

Dokończ

Bogdan:

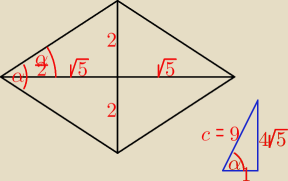
	α		2
Albo: α∊(0o, 90o), tg		=		,
	2		√5

	α   2*tg   2		2   2*   √5
tgα =		=		= 4√5
	α   1 − tg2   2		4   1 −   5

	1
c= √1 + 80 = 9, cosα =		,
	9

	1
tgα + 9cosα = 4√5 + 9*		= ...
	9

Eta: A może tak a=3

	4*2√5		4√5
P(rombu)=		= 4√5 i P=a2*sinα ⇒ 9sinα=4√5 ⇒ sinα=
	2		9

	1
cosα= √1−sin2α =....=
	9

	sinα
tgα=		=....... = 4√5
	cosα

Eta: tgα+9cosα=4√5+1

Eta:

Bogdan:

Eta:

James: Dziękuje bardzo