Trygonometria. trapez. James: Długości podstaw trapezu są równe 5 i 20 a jego przekątne przecinają się pod kątem prostym. Oblicz cosinusy kątów nachylenia przekątnych do dłuższej podstawy, jeśli wysokość trapezu jest równa 12.

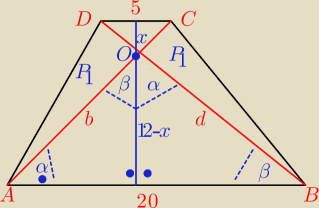
Janek191: Z podobieństwa trójkątów Δ CDO i Δ ABO mamy

5		20
	=
x		12 − x

20 x = 5&(12 − x) = 60 − 5x 25 x = 60 x = 2,4 h = 12 − x = 12 − 2,4 = 9,6 Pole Δ ABO P = 0,5*20*9,6 = 96 oraz

	192
P = 0,5 b*d = 96 ⇒ b*d = 192 ⇒ d =
	b

i z Tw. Pitagorasa b² + d² = 20² = 400

	1922
b2 +		= 400 / * b2
	b2

b⁴ − 400 b² + 192² = 0 b⁴ − 400 b² + 36 864 = 0 Δ = 160 000 − 4*1*36 864 = 160 000 − 147 456 = 12 544 √Δ = 112

	400 − 112		400 + 112
b2 =		= 144 lub b2 =		= 256
	2		2

więc b = 12 lub b = 16

	192		192
d =		= 16 lub d =		= 12
	12		16

zatem mamy

	h		9,6
cos α =		=		= 0,6
	d		16

	h		9,6
cos β =		=		= 0,8
	b		12

===================

James: Dziękuje bardzo

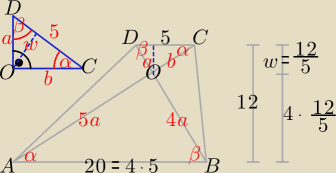
Bogdan: Moja propozycja rozwiązania tego zadania:

	20
Skala podobieństwa trójkątów prostokątnych ABO i CDO jest równa		= 4
	5

w − wysokość w trójkącie COD opusczona z wierzchołka kąta prostego O na bok CD.

	1		12		a*b
w =		*12 =		=		⇒ 2*a*b = 24 i a2 + b2 = 25, a, b > 0
	5		5		5

(a + b)² = a² + 2ab + b² = 25 + 24 = 49 ⇒ a + b = √49 = 7 Jeśli a+b=7 i ab = 12 to z wzorów Viete'a otrzymujemy x²−7x+12=0 ⇒ (x − 3)(x − 4) = 0 Stąd a = 3 i b = 4 lub a = 4 i b = 3,

	4		3
cosα =		i cosβ =		lub odwrotnie.
	5		5