Trójkąt o bokach 6,8,12 i Trygonometria Rekkles: Dany jest trójkąt bokach 6,8,12 . Zbadaj korzystając z tw.cos czy trójkąt jest prostokątny,rozwartokątny, czy ostrokątny.Oblicz długość części dwusiecznej najmniejszego kąta zawartej w trójkącie.Oblicz dł. promienia opisanego na tym trójkącie Pomoże ktoś ?

Piotr 10: Po co twierdzenie kosinusów ? Wystarczy, że policzymy kwadraty długości boków a=6 , a²=36 b=8 , b² = 64 c=12 c²= 144 A więc c² > a²+b² ,bo 144 > 100

Piotr 10: Czyli jest to Δ rozwartokątny

5-latek: Piotr ale ma napisane ze ma korzystac z tego tweirdzenia to musi korzystac

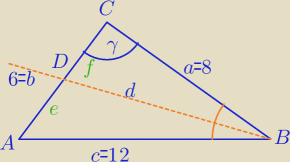
Mila: 1) 0<γ<180 12²=6²+8²−2*6*8 *cosγ⇔ 144=36+64−96 cosγ 44=−96 *cosγ

	44		11
cosγ=−		=−		<0 zatem γ>90o ⇔ΔABC jest trójkątem rozwartokątnym.
	96		24

2) długość odcinka dwusiecznej Z tw. o dwusiecznej:

e		f
	=		i e+f=6
12		8

	3
e=		f
	2

3
	f+f=6
2

	12		18
f=		i e=
	5		5

Z tw. cosinusów w ΔCDB:

	12		12
d2=(		)2+82−2*		*8*cosγ
	5		5

	144		24		11
d2=		+64−		*8*(−		)
	25		5		24

d²=5,76+64+17,6 d²=87,36 d=√87,36 3) R− promień okręgu opisanego na ΔABC

	a*b*c
PΔABC=
	4R

	a*b*c
R=
	PΔABC

oblicz pole Δ i podstaw, poradzisz sobie?

Lukas: Mila masz za dobre serce