pochodna z modułem
john2: pochodna (|sinx|)'
Tak to ma wyglądać?
1) sinx ≥ 0
x ∊ <2kπ, π + 2kπ>
(|sinx|)' = (sinx)' = cosx
2) sinx < 0
x ∊ (π + 2kπ, 2π + 2kπ)
(|sinx|)' = (−sinx)' = −cosx
11 wrz 16:42
john2: Czy może tak?
| | 1 | | 1 | |
(|sinx|)' = (√sin2x)' = |
| * (sin2x)' = |
| * 2sinx * (sinx)' = |
| | 2√sin2x | | 2√sin2x | |
| | 1 | | 2sinxcosx | | sin2x | |
= |
| * 2sinxcosx = |
| = |
| |
| | 2√sin2x | | 2√sin2x | | 2√sin2x | |
11 wrz 16:52
Mila:
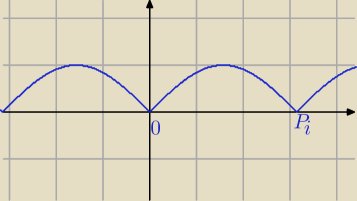
Musisz zbadać z definicji, czy czy istnieje pochodna dla x=kπ.
11 wrz 17:45
J:
| | sin2x | |
.... przychyliłbym się do zapisu: (IsinxI)' = |
| ... bo pokazuje,gdzie pochodna |
| | 2IsinxI | |
nie istnieje
11 wrz 17:50
john2: ok, więc:
| | f(x0 + Δx) − f(x0) | | f(kπ + Δx) − f(kπ) | |
limΔx−>0 |
| = limΔx−>0 |
| = |
| | Δx | | Δx | |
| | |sin(kπ + Δx)| − |sin(kπ)| | |
= limΔx−>0 |
| = co z tym zrobić? |
| | Δx | |
11 wrz 18:00
Mila:
Podpowiedź do pochodnej z definicji.
|sinkπ|=0
|sin(kπ+Δx)|=|sinkπ*cos Δx+sinΔx*coskπ|
11 wrz 18:09
john2: Wybacz, ale chyba na zbyt głęboką wodę się rzuciłem
| | |sinkπ *cosΔx + sinΔx*coskπ| | |
limΔx −> 0 |
| i znowu nie wiem |
| | Δx | |
poza tym to badanie to jest kontynuacja do mojego pierwszego postu?
Czy mój drugi post wystarczy, jak chyba napisał J?
11 wrz 18:30
john2: choć może wiem, moment
11 wrz 18:31
john2: nie, jednak nie wiem
11 wrz 18:31
Mila:
cd 18:29
sin(kπ)=0
| | |0*cos(Δx)+sin(Δx)*cos(kπ)| | |
limΔx→0 |
| = |
| | Δx | |
| | |sin(Δx)| | |
=limΔx→0{ |
| *|cos(kπ)|= |
| | Δx | |
=1 dla Δx→0
+
=−1 dla Δx→0
−
11 wrz 22:35
john2: No tak. Dziękuję. Możesz jeszcze napisać, czy mój post z 16:52 jest w ogóle potrzebny?
12 wrz 07:57
Mila:
Jest w porządku. Też wyjdzie .
12 wrz 16:05
john2: Dzięki jeszcze raz.
12 wrz 16:13