Na sprawdzian bedzie takie 3 klasa liceum
Mika: Przprowadź dyskusje liczby rozwiazan równania 2|x|−1=−2m+1 ze względu na wartość parametru
m, m ∊R. Następnie naszkicuj wykres funkcji y=g(m), która każdej wartości parametru m
przyporządkowuje liczbę rozwiązań danego równania.
11 wrz 11:44
J: | | 1 | |
No to przedyskutujmy.... ile będzie rozwiązań dla m = |
| ..? |
| | 2 | |
11 wrz 12:01
Piotr 10:
| 2 | | 2 | | 2 | |
| →T u→[1,0] → |
| → Wb0Y→ |
| |
| x | | x − 1 | | IxI−1 | |
Narysuj wpierw ten wykres funkcji
11 wrz 12:04
mika: I.co teraz
11 wrz 12:55
Godzio:
| | 3 | |
Dla −2m +1 = −2 mamy jedno rozwiązanie czyli m = |
| |
| | 2 | |
itd.
11 wrz 12:58
g:
| | 2 | |
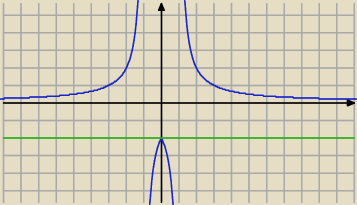
Narysuj wykres p(x) = |
| . Następnie prowadź poziome linie i sprawdzaj ile mają |
| | |x| − 1 | |
punktów wspólnych z wykresem. Niech poziome linie będą określone jako.
p
1(x) = a
1
p
2(x) = a
2
p
3(x) = a
3
.
.
.
Należy ocenić ile punktów wspólnych ma wykres p(x) z wykresami p
1(x), p
2(x), p
3(x)... a
następnie rozwiązać równania:
a
1 = −2m + 1
a
2 = −2m + 1
a
3 = −2m + 1
.
.
.
i udzielić prawidłowej odpowiedzi
11 wrz 13:01
pigor: ..., lub tak :
2|x|−1 = −2m+1 i |x|−1≠0 ⇒ 2=(1−2m)(|x|−1) ⇒
⇒ |x|−1=
21−2m≠0 i |x|−1≠0 i 1−2m≠0 , teraz narysuje sobie
funkcję
y=|x|−1≠0, bez punktów (−1,0) i (1,0) i z jej wykresu
czytaj i rozwiązuj nierówności i rysuj wykres funkcji g :
1)
21−2m ≤ −1 ⇒ g(m)= ?
2) 1<
21−2m < 0 ⇒ g(m) ?
3)
21−2m = 0 ⇒ g(m)= ?
4)
21−2m > 0 ⇒ g(m)= ? g. przedziałami liniowa − stała .

11 wrz 13:31
mika: m=
32
Godzio narysował wykres i okej. Punkt jest −2. A co z górna częścią wykresu? Tam nie na
określonego punktu jak w dolnej części wykresu. Mają być przedziały

11 wrz 13:35
Mika: 

?
11 wrz 14:18
J: Przesuwaj równolegle do osi OX linijkę i patrz w ilu miejscach przecina wykres w zależności od
rzędnej, która w tym przypadku musi być równa : −2m +1
11 wrz 14:21
Mika: Można bardziej jaśniej?
11 wrz 14:23
J:
Popatrz na zieloną linię poziomą ... ma ona jeden punkt wspólny z wykresem , czyli jest jedno
| | 3 | |
rozwiązanie , przecina ona oś OY w punkcie y = − 2 , stad: −2m + 1 = − 2 ⇔ m = |
| , |
| | 2 | |
zatem dla m = U{3}[2} istnieje tylko jedno rozwiazanie
11 wrz 14:28
Mika: ROzumiem ale górna część wykresu nie ma konkretnego punktu, tylko przedziały
11 wrz 14:29
Mika: 
?
11 wrz 16:35
J:
W dół od zielonej − 2 rozwiązania
Pomiędzy zieloną i osią OX − brak rozwiązań
Powyżj OX − 2 rozwiązania
11 wrz 16:43
Mika: Jak to zapisać z tym −2m+1"?
11 wrz 16:49
J:
−2m+1 < −2 (oblicz m ) − 2 rozw.
− 2 < −2m+1 < 0 (oblicz m ) − brak
−2m+1 > 0 (oblicz m ) − 2 rozw.
11 wrz 16:51
Mika: 10
−2m+1<−2
2m>3
m>32
dla m >32 2 rozwiązania
20 −2<−2m+1
−2m+1<0 2m<3
2m>1 m<32
m>12
Brak rozwiązania
30
−2m+1>0
−2m>−1
2m<1
m<12
dla m<12 2 rozwiązania
Taka jest odpowiedź?
11 wrz 17:00
J: | | 3 | |
Jeszcze dla m = |
| − 1 rozw. |
| | 2 | |
11 wrz 17:02
Mika: 10
−2m+1<−2
2m>3
m>32
dla m >32 2 rozwiązania
20 −2<−2m+1
−2m+1<0 2m<3
2m>1 m<32
m>12
Brak rozwiązania
30
−2m+1>0
−2m>−1
2m<1
m<12
dla m<12 2 rozwiązania
40
−2m+1=−2
2m=3
m=32 1 rozwiązanie
To są końcowe odpowiedzi?
11 wrz 17:07
J:
Tak ...
Na końcu , to masz jeszcze narysować funkcję y = g(m)
11 wrz 17:08
Mika: W jaki sposób mam to zrobić? Podasz przykład?
11 wrz 17:11
J:
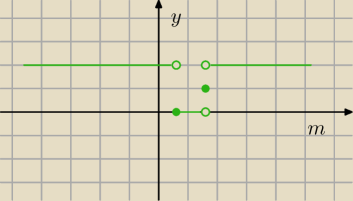
11 wrz 17:12
Mika: Jak najdokładniej zapisac te y=g(m)

? matematycznie oczywiscie
11 wrz 17:18
Mika: 
11 wrz 19:54
mika: W jaki sposób ten wykres naszkicowales

Jeśli można to proszę o wyjaśnienie krok po kroku
11 wrz 23:16
mika: Ktoś pomoże?
12 wrz 08:19
J:
Patrz na wykres.... (zielona linia)
| | 1 | |
Dla m ∊ (−∞, |
| ) − y = 2 ( 2 rozwiązania)
|
| | 2 | |
| | 1 | | 3 | |
Dla m ∊ < |
| , |
| ) − y = 0 (brak rozwiązań)
|
| | 2 | | 2 | |
| | 3 | |
Dla m = |
| − y = 1 ( 1 rozwiązanie)
|
| | 2 | |
| | 3 | |
Dla m ∊ ( |
| ,+∞) − y = 2 (2 rozwiązania)
|
| | 2 | |
12 wrz 08:21
mika: Super, dziękuję
12 wrz 08:27
Mika: Coś jest nie tak z nawiasami w odpowiedzieach bo w odpowiedziach jest 0 rozwiązań dla m∊<
Co jest nie tak z pierwszym nawiasem?
12 wrz 08:58
J: Przecież dokładnie tak Ci napisałem...
12 wrz 09:04
Mika: No tak ale wcześniej napisałeś 0 rozwiązać dla −2<−2m+1<0 przy takich nawiasach jest chyba
przedział otwarty?
12 wrz 09:07
J: ... OK ...miało być: − 2 < −2m +1 ≤ 0
12 wrz 09:10
Mika: Hha ok juz nie narzekam
12 wrz 09:11
Kacper: A samemu nie możesz pomyśleć jak być powinno?

12 wrz 09:11
Mika: Pomyślałem i dlatego napisalem.
12 wrz 09:16




 ?
?
 ?
?

 ? matematycznie oczywiscie
? matematycznie oczywiscie

 Jeśli można to proszę o wyjaśnienie krok po kroku
Jeśli można to proszę o wyjaśnienie krok po kroku
