jak takie zadania się rozwiązuje proszę o rozwiązanie: wyznacz zbiór wartości funkcji f jeśli 1) f(x) = ²_3^x+1 2) f(x) = ^2x+4_2^x+1 wiem że trzeba określić dziedzinę czyli dla 1) 3^x + 1 ≠ 0 ⇒ 3^x ≠ −1 ⇒ x≠ 0 a w drugim 2^x +1 ≠ 0 ⇒ x≠ 0 ale jak dalej

J: W obydwu przypadkach dziedziną jest R. Zapisz jeszcze raz uzywajć do ułamka dużego U

Janek191:

	2
1) f(x) =		?
	3x + 1

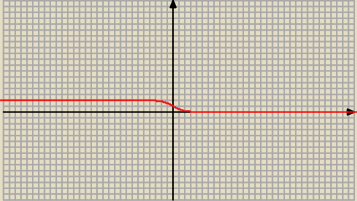
lim f(x) = 0 x→ + ∞ lim f(x) = 2 x → −∞ f ' ( x) < 0 − funkcja maleje w ℛ więc ZW_f = ( 0 ; 2 ) ================

proszę o rozwiązanie: ale ja nie miałem ani pochdnych ani granic tyle tylko że przeględłem podręcznik jeszcze raz napiszę zadania

	2
1) f(x) =
	3x+1

	2x+4
2)f(x) =
	2x+1

...: w 2) niby dlaczego x≠0 ?

J: Można dojść do wyniku bez pochodnych i granic, znając funkcję wykładniczą y = a^x .... jeśli tej funkcji nie znasz, to nie jesteś w stanie rozwiązac tego zadania..

...: 2)

	3
f(x)=1+
	2x+1

i teraz chyba jaśniej

proszę o rozwiązanie:

	2x+4
2)f(x) =
	2x+1

2^x+1 ≠ 0⇒ 2^x ≠ −1⇒ 2^x ≠ −2⁰⇒ x≠0 nie wiem co z tym minusem może rzeczywiście robię coś żle

J: Wyrażenia: 2^x +1 oraz 3^x + 1 ... przyjmują tylko wartości dodatnie dla kazdego x.

...: ... zupełnie ŹLE −

...:

	1+4
zauważ, że w 2) f(0)=		=2,5
	1+1

proszę o rozwiązanie: masz rację czyli w zadaniu 1) 2(2^x+1)>0 a w drugim zadaniu (2^x+4)(2^x+1) >0 czy to należy rozwiązać

J: Jeszcze raz ... w obydwu zadaniach dziedzina: D = R , bo mianownik nigdy się nie zeruje...

...: ... nie ... trzeba włączyć myślenie − 1) Jakie wartości przyjmuje f(x)=2^x 2) a jakie f(x)=2^x+1

	3
3) czyli f(x)=		przyjmuje jakie?
	2x+1

	3
4) ostatecznie f(x)=1+		jakie?
	2x+1

proszę o rozwiązanie: bardzo dziękuję już wiem

...: −