? marlę: trygonometria Mógłby mi ktoś wytłumaczyć dlaczego w równaniu

	1
cos2x =
	4

	π		π
otrzymujemy wynik −		+ kπ ⋁		+ kπ
	3		3

Chodzi mi konkretnie dlaczego jest kπ, skoro okres cosx to 2kπ ?

Mila:

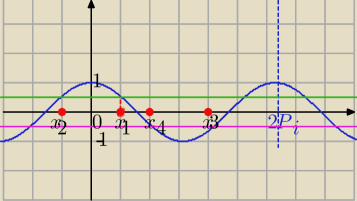
	1		1
cosx=		lub cosx=−		⇔
	2		2

	π		π		4		2
x1=		+2kπ lub x2=−		+2kπ lub x3=		π+2kπ lub x4=		π+2kπ
	3		3		3		3

Jeśli spojrzysz na oś liczbową to zauważysz, że można to krócej zapisac. Jeśli zapiszesz 4 rozwiazania z okresem 2π to też będzie dobrze.

pigor: ... , bo może nie lubi modułu (wart. bezwzgl.) i zamiast np. tak : cos²x=¹₄ ⇔ |cosx}= ¹₂ ktoś (autor zadania+odpowiedzi) rozwiązywał sobie tak : cos²x= ¹₄ /*2 ⇔ 2cos²x= ¹₂ ⇔ 1+cos2x= ¹₂ ⇔ ⇔ cos2x= −¹₂, a tu mamy właśnie okres π (kπ).

marlę: dzięki wielkie

Mila: