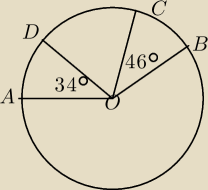
Kąty w okręgu. Wiecheć: Dany jest okrąg o środku O oraz miary dwóch kątów środkowych. Wyznacz, pod jakim kątem rozwartym przecinają się odcinki AC i BD. Chodzi zapewne o coś z kątami wewnętrznymi, będę bardzo wdzięczny za jakiekolwiek wskazówki od czego zacząć.

Jolanta: narysuj sobie te odcinki masz trójkąt suma katów=180⁰ kąt ACD=17 ⁰ bo jest oparty na tym samym łuku co kat AOD Kąt BDC=23⁰

asiunia: Jak połączysz A z C i B z D, to szukanym kątem będzie ten rozwarty utworzony przez przecięcie się |AC| i |BD| Mamy dwa trójkąty równoramienne o ramieniu równym promieniowi: ΔOCB i ΔOAD Możemy więc, obliczyć kąty ΔOCB przy podstawie, czyli ∡OCB i ∡OBC

180−46
	= 67
2

i kąty przy podstawie w ΔOAD, czyli ∡ODA i ∡OAD

180−34
	= 73
2

Teraz widzimy, że ∡ADB i ∡ACB oprte są na tym samym łuku i wychodzą z tych samych punktów A i B, więc są równe oznaczamy ∡ODB=α i ∡OCA=β piszemy zależność kątów: α+73 = β+67 β= 73 − 67 + α β= 6 + α Zauważmy kolejny trójkąt równoramienny o ramionach r, czyli ΔOAC, którego kąty przy podstawie są równe β, a po podstawieniu 6+α Skupmy się teraz na trójkącie równoramiennym OAD, gdzie właśnie kąt 6+α jest częścią kąta o mierze 73. Szukamy w takim razie drugiej części tego kąta 73 − (6 +α) 73 − 6 − α ten kąt ma miarę 67 − α Następnie rozpatrzamy mały trójkącik o jednym z boków |AD|,a dwa pozostałe utworzone są przez przecinające się odcinki |AC| i |OD|. Mamy wyliczone w nim dwa kąty: 73 oraz 67−α Trzeci w takim razie wynosi 40+α Ostatnim trójkącikiem, w którym musimy wyliczć kąty jest ten leżąc obok rozpatrzanego poprzednio i o jednm z kątów równym α i jednym rozwartym. Kąt rozwarty test dopełnieniem do 180 dla kąta 40+α, wieć wynosi 140−α. Mając dane dwa kąty, wyiczamy trzeci, który wychodzi nam 40. Kąt 40 jest dopełnieniem do 180 dla naszego szukanego kąta, wiec nasz kąt rozwarty utworzony przez przecięcie się |AC| i |BD| ma miarę 140.