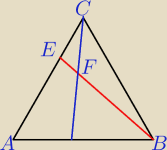
 W trójkącie ABC punkty D, E leżą odpowiednio na bokach AB i AC tak, że |AD| : |DB| = 1:2 oraz
|AE| : |EC| = 2:1. Udowodnij, że |EF| : |FB| = 1:6.
Będę bardzo wdzięczny za wszelkie wskazówki!
W trójkącie ABC punkty D, E leżą odpowiednio na bokach AB i AC tak, że |AD| : |DB| = 1:2 oraz
|AE| : |EC| = 2:1. Udowodnij, że |EF| : |FB| = 1:6.
Będę bardzo wdzięczny za wszelkie wskazówki!
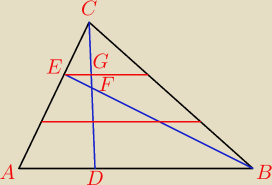 Dzięki dorysowaniu tych dwóch czerwonych linii, udało mi się znaleźć kilka trójkątów podobnych
po lewej stronie oraz, przede wszystkim, sprawdzić, iż trójkąt oznaczony przeze mnie EFG jest
podobny do trójkąta BDF. Wg treści zadania skala podobieństwa powinna wynieść 1:6. Ktoś ma
jakiś pomysł jak to udowodnić?
Dzięki dorysowaniu tych dwóch czerwonych linii, udało mi się znaleźć kilka trójkątów podobnych
po lewej stronie oraz, przede wszystkim, sprawdzić, iż trójkąt oznaczony przeze mnie EFG jest
podobny do trójkąta BDF. Wg treści zadania skala podobieństwa powinna wynieść 1:6. Ktoś ma
jakiś pomysł jak to udowodnić?
| 1 | ||
Więc, skoro wiemy, że ΔEFG~ΔBDF, a skala podobieństwa k ma być równa | , to napiszmy | |
| 6 |
| |EF| | |EG| | |GF| | 1 | |||||
k= | = | = | = | |||||
| |FB| | |DB| | |FD| | 6 |
| y | 3x | xy | x | ||||
= | ⇒ z = | = | = |EG| | ||||
| z | x | 3y | 3 |
| 1 | ||
podstawiamy do k, by wykazać, że sala podobieństwa wynosi | ||
| 6 |
| |EG| | z |
| 1 | |||||||||||
k= | = | = | = | ⇒ |EF| : |FB| = 1 : 6 | ||||||||||
| |DB| | 2x | 2x | 6 |
| y | 3y | ||
= | |||
| z | x |