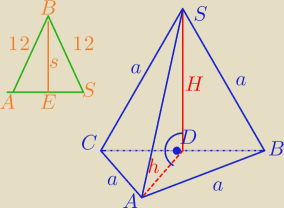
Pole powierzchni całkowitej ostrosłupa. Azta: Treść zadania to: Podstawą ostrosłupa jest trójkąt równoboczny o boku długości 12 cm. Jedna ściana boczna tego ostrosłupa jest trójkątem równobocznym i jest prostopadła do płaszczyzny podstawy. Oblicz pole powierzchni całkowitej i objętość tego ostrosłupa. Mam problem z obliczeniem pola ścian bocznych, które nie są równoboczne. Mają one dwie krawędzie po 12 cm i jedną niewiadomą. Czy policzenie jej z twierdzenia Pitagorasa (korzystając z wysokości podstawy i prostopadłej do niej ściany) i później podstawienie jej do wzoru Herona byłoby dobrym pomysłem? Dodam, że wynosi ona wtedy 6√3

Mila: H=h=6√3 ΔADS−Δ prostokatny równoramienny |AS|=6√3*√2=6√6 ΔASB≡ΔASC − Δrównoramienne. ES=3√6 12²=s²+(3√6)² 144=s²+54 s²=90 s=√90=3√10

	1
PΔASB=		*6√6*3√10=9√60=9*2√15
	2

	122√3
Pb=		+2*18√15
	4

P_b=36*(√15+√3)