Nie ogarniam L: Wewnątrz kąta o miere 60⁰ znajduje się punkt A odległy od jednego z ramion o 3, a od drugiego o 6. Oblicz długość punktu A od wierzchołka kąta.

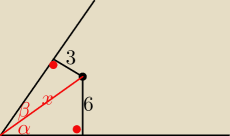
Nieznajomy: α+β=60

	6
sinα=
	x

	3
sinβ=
	x

	36		x2−36
cos2α = 1−		=
	x2		x2

	9		x2−9
cos2β = 1−		=
	x2		x2

	1
cos(α+β) = cos60 =
	2

cos(α+β) = cosα*cosβ − sinα*sinβ stąd

√x2−36		√x2−9		6		3		1
	*		−		*		=		/*x2
x		x		x		x		2

	x2
√x2−36*√x2−9 − 18 =
	2

	x2
√x2−36*√x2−9 =		+ 18 /()2
	2

	x4
(x2−36)(x2−9) =		+ 18x2 + 182
	4

	x4
x4 − 45x2 + 9*36 =		+ 18x2 + 182 /*4
	4

4x⁴ − 180x² + 36² = x⁴ + 72x² + 4*18² 3x⁴ − 252x + 36² − 4*18² = 0 i rozwiązać, ale powinien być prostszy sposób

PW: Gdyby to umieścić w układzie współrzędnych tak, by wierzchołek kąta był początkiem układu, a jedno ramię stanowiło dodatnią półoś OX, to drugie ramię będzie zawarte w prostej o równaniu (1) y = √3x. Niech A = (a, 3) (bo jest odległy o 3 od osi OX). Jeżeli znasz wzór na odległość punktu od prostej (1) (a ma ona być równa 6), to wyliczysz współrzędną a punktu A i odległość AO o którą pytają w zadaniu.

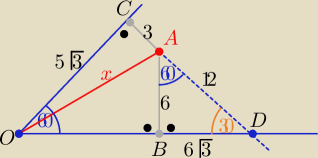
Znajomy: Ze związków miarowych w trójkątach o kątach 30^o,60^o,90^o w ΔBAD i ODC |AD|=12 , |OC|=5√3 i |DC|=15 z tw. Pitagorasa w Δ AOC x>0 x²= 9+75 ⇒x= 2√21 Pozdrawiam Wszystkich "Nieznajomych"

Znamy się tylko z widzenia :

	1
sin30o=
	2

1		3
	=
2		|AE|

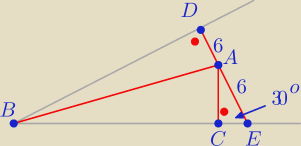
|AE|=6 |CE|²=6²−3² |CE|=3√3

	√3
sin60o=
	2

√3		12
	=
2		|BE|

|BE|=8√3 |BC|=|BE|−|CE| |BC|=5√3 |AB|²=3²+(5√3)² |AB|=2√21

Znamy się tylko z widzenia : Eta ?

Znajomy: