Wzajemne położenie prostej i okręgu. Styczna do okręgu. - Geometria analityczna
Leszek: Witam,
Okrąg przechodzi przez punkt A(4,1), zaś jego środek należy do prostej k: x−y=0. Wiedząć, że
okrąg ten jest styczny do prostej l: y−5=0, wyznacz jego równanie.
Nie mam kompletnie pojęcia jak się zabrać za to zadanie. Jakaś pomoc?
Dziękuję z góry.
7 wrz 23:30
Janek191:
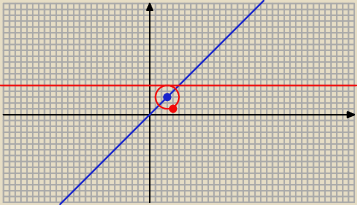
7 wrz 23:36
Janek191:

7 wrz 23:37
Janek191:
A = ( 4; 1)
S = ( a ; a ) − bo S leży na prostej o równaniu y = x
( x − a)2 + ( y − a)2 = r2
y = 5 − równanie prostej stycznej
zatem
( x − a)2 + ( 5 − a)2 = r2
( 4 − a)2 + ( 1 − a)2 = r2 − przechodzi przez A = ( 4; 1)
x2 − 2a x + a2 + 25 − 10 a + a2 = r2
16 − 8 a + a2 + 1 − 2a + a2 = r2
x2 − 2a x − 10 a + 2a2 + 25 = r2
− 10 a + 2 a2 + 17 = r2
x2 −2a x + 8 = 0
Δ = 4a2 − 4*1*8 = 4 a2 − 32 = 0 ⇒ a2 = 8 ⇒ a = 2√2
czyli
S = ( 2√2 ; 2√2)
r = 5 − 2√2 ⇒ r2 = 25 − 20√2 + 8 = 33 − 20√2 ≈ 4,7
dlatego równanie okręgu ma postać
( x − 2√2)2 + ( y − 2√2)2 = 33 − 20√2
==================================
7 wrz 23:56

