proszę o odpowiedż proszę o rozwiązanie: powracam do zadania wyznacz zbiór wartości funkcji f jeśli f(x) = −36^x −4 * 6^x −5 ( wynik ZW =( −∞ , −5) ) ja to wykonałem tak 6^x =t dla t > 0 −t² −4t −5 > 0 Δ < 0 t_w = −2 i nie wiem jak dojść do wyniku bez liczenia granic podobnie jest z zadaniem f(x) = ⁻²_9^x − ⁸_3^x − 12 ( wynik ZW = ( −∞ , −12 ) i ten sam problem bo wykonałem tak 3^x = t dla t > 0 ⁻²_t² − ⁸_t − 12 I t² − 12t² −8t −2 >0 Δ < 0 t_w = − ¹₃

Mila:

	2		8
2) f(x)=		+		−12, czy to taka funkcja?
	9x		3x

proszę o rozwiązanie: słusznie nie taka już poprawiam f(x) = ⁻²_9^x − ⁸_3^x − 12 ale w zadaniu 1 ZW jest w odpowiedzi przedziął obustronnie otwarty

Mila: 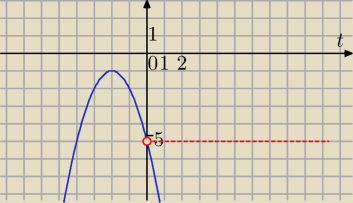Poprawka. 1) f(t)= −t²−4t−5 i t>0 tw=−2 f(−2)=−4+8−5=−1 tw<0 f(t) malejąca dla t>−2 f(0)=−5 Zw= (−∞,−5) (2) źle widać w mojej przeglądarce. Może zapisz to inaczej, bo tak to nie pomogę.

proszę o rozwiązanie: powracam do zadania 1 chyba tam nie ma być f(0) = −5 bo jak wstawimy do funkcji f(0)= − 36⁰ − 4 * 6⁰ −5 ≠ −5 tylko g(t) = −5 bo g(0) = − 0² −4*0 −5 = −5 czy dobrze myślę

Mila: Dobrze myślisz. Jednak dla ustalenia zbioru wartości tak liczymy jak podałam 20:41 t>0 to f(t)<f(0)=−5 ponieważ f(t) to funkcja malejaca dla t>−2

proszę o rozwiązanie: dziękuję ale powracam do zapisu zadania 2 f(x) = −2/ 9^x − 8 / 3^x − 12 / oznacza że −2 jest w liczniku a w mianowniku 9^x to samo 8 jest w liczniku a w mianowniku 3^x

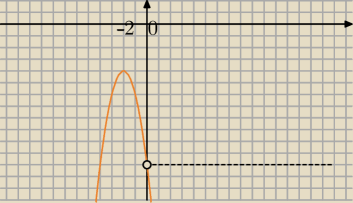
Mila: 9^x=(3^x)²

	1
(		)x=t, t>0
	3

f(t)=−2*t²−8t−12, t>0

	8
tw=		=−2
	−4

f(t) jest funkcją malejącą dla t>−2 t>0 to f(t)<f(0)⇔f(t)<−12

proszę o rozwiązanie: dziękuję za wykonanie

Mila:

proszę o rozwiązanie: jeszcze mam jednozadanie proszę osprawdzenie f(x) = 1 / 2*25^x − 5^−x + 1/2 1/2t² − 1/t + t² > 0 I * 2t² i t >0 t_w = 1 1 − 2t + t² >0 Δ = 0 t>0 to f(t) >0 czyli ZW = < 0, +∞) proszę o sprawdzenie

proszę o rozwiązanie: żle zapisałem powinno być 1/2t² − 2t + 1/2 >0 I * 2t² 1− 2t + t² > 0 i dalej tak jak zapisałem

Mila: Nie możesz tak mnożyć przy wyznaczaniu zbioru wartości funkcji, bo zmieniasz funkcję.

	1		1
f(x) =		*25x−5−x+		taki wzór ?
	2		2

proszę o rozwiązanie: nie 25^x jest też w mianowniku zapisze to jeszcze raz f(x) = ¹_2*25^x − 5^−x + ¹₂

Mila:

	1
(		)x=t, t>0
	5

	1		1
f(t)=		*t2−t+
	2		2

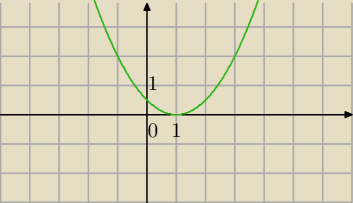
t_w=1 1>0 dla t=1 f(t) ma wartość najmniejszą

	1		1
f(t)=		−1+		=0 wartość najmniejsza f(x)
	2		2

f(t) jest rosnaca dla t>1 Z_wf=<0,∞)

	1		1		1		1
limx→∞		−		+		=
	2*9x		5x		2		2

	1		1		1
limx→−∞		−		+		=∞
	2*9x		5x		2

proszę o rozwiązanie: dlaczego w granicy w mianowniku jest 9^x a nie 25^x jeżeli zadanie dotyczy powyższego zadania i dlaczego w granicy lim _X→ − ∞= −∞ a nie ¹₂

Mila: Nie mogłam porawić wczoraj, bo strona mi nie wchodziła. Zamiast 9^x ma być 25^x.

proszę o rozwiązanie: czyli granica ma byc równa ¹₂ a nie minus nieskończoność

Mila: Nigdzie nie napisałam, ze granica (−∞)

	1		1
limx→−∞		*25−x−5−x+		=∞
	2		2

	1		1		1
limx→∞		*25−x−5−x+		=
	2		2		2

Mila:

	1		1
f(x)=		−5−x+
	2*25x		2

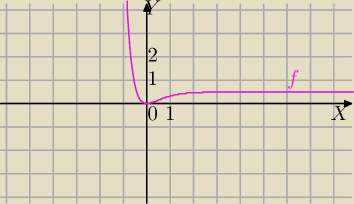
Nie wiem, czy dobrze widać, w mianowniku jest 2*25^x.

proszę o rozwiązanie: chodzi mi o te granice , dlaczego w 1) nie ma wyniku ¹₂ a jest nieskończoność 1) limx→−∞ ¹₂ *25^−x −5^−x + ¹₂ = ∞ 2) limx→∞ ¹₂ *25^−x −5^−x +¹₂ = ¹₂

Janek191:

	1		1
12 *25−x − 5−x + 12 = 12*		−		+ 12
	25x		5x

	1
lim 25x = 0 ⇒ lim		= + ∞
	25x

x→ −∞ x→ −∞ Podobnie lim 5^−x = +∞ x→ −∞ Ponieważ 25^−x znacznie szybciej rośnie niż 5^−x , więc różnica 25^−x − 5^−x rośnie też do +∞

proszę o rozwiązanie: dziękuję bardzo

proszę o rozwiązanie: przeprasza ze jestem dociekliwy ale dalej męczy mnie zad 2 zgadzam się z Jankiem 191 końcowy wynik zad 2 jest 1/2 a w drugim ∞ 1) lim _{X →} −_∞ = ¹₂*25^−x −5 ^−x + ¹₂ = − ∞ 2) lim_x→+∞ = ¹₂*25^−x −5 ^−x + ¹₂ =¹₂ czyli granica funkcji f jest równa ∞ czy ¹₂

Mila:

	1		1
Popatrz na wykres f(x)=		*25−x−5−x+
	2		2

	1		1		1
limx→∞[		*25−x−5−x+		]=
	2		2		2

natomiast

	1		1
limx→−∞[		*25−x−5−x+		]=∞
	2		2

Ty znowu źle zapisałeś (1) 16:30 O jaką granicę pytasz ? W nieskończoności− w (+∞) czy w (−∞)?

	1
Co masz na myśli " końcowy wynik"		?
	2

proszę o rozwiązanie: chodzi mi o to że jeżeli granica dąży do +∞ to wynosi 1/2 a jeżeli granica dąży do − ∞ to wynosi − ∞

Mila: Granice są takie jak napisałam 20:32. To samo napisał Janek z dokładnym wyjaśnieniem. Jesteś studentem, czy licealistą? Nie granica dąży do ∞

	1
tylko x→∞ wtedy g=
	2

x→−∞ wtedy granica f(x) jest równa ∞

proszę o rozwiązanie: dziękuję

proszę o rozwiązanie: odpisuję jestem uczniem 3 klasy i nie miałem jeszcze granic tyle tylko c0 wyczytałem z podręcznika

Mila: W takim razie, poczekaj z granicami do lekcji z tego działu, bo źle się sam nauczysz i będziesz utrwalał błędy.

proszę o rozwiązanie: wyznacz zbiór wartości funkcji

	−2*5x −7
f(x) =		ale bez obliczania granic
	5x +4

	3
wynik to ZW = ( −2 , − 1		)
	4

proszę o rozwiązanie: mam jeszcze jedno zadanie

	−2*5x −7
Wyznacz zbiór wartości funkcji f(x) =
	5x +4

bez obliczania granic

	3
wynik to ZW = ( −2 , −1		)
	4

J:

	4
..mnie wychodzi : ZW = (−2, −1		)
	5

ZKS:

−2 * 5x − 7		−2(5x + 4) + 1		1
	=		=		− 2
5x + 4		5x + 4		5x + 4

0 < 5^x < ∞ 4 < 5^x + 4 < ∞

1		1
	>		> 0
4		5x + 4

	7		1
−		>		− 2 > −2
	4		5x + 4

proszę o rozwiązanie:

	1		7
skąd z ∞ jest 0 a potem z		jest −
	4		4

Mila:

	−2*5x−7
f(x)=
	5x+4

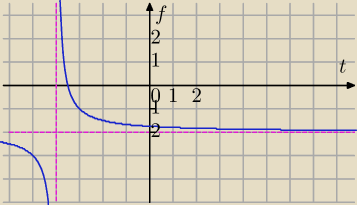
5^x=t, t>0

	−2t−7
f(t)=		funkcja homograficzna, przekształcamy do postaci kanonicznej
	t+4

	−2*(t+4)+8−7
f(t)=
	t+4

	1
f(t)=		−2
	t+4

dwie asymptoty dla t∊R\{−4} x=−4 pionowa y=−2 pozioma Nas interesuje tylko ta część wykresu, która odpowiada argumentom dodatnim.funkcja jest malejąca dla t>0.

	1		3
f(0)=−2+		=−1
	4		4

dla t>0

	−7
−2<f(t)<		zbiór wartości f(x) to
	4

	−7
Zwf=(−2,		)
	4

proszę o rozwiązanie: dziękuję teraz to jest zrozumiałe

Mila: Załóż nowy wątek do następnego zadania, bo długo się przewija.

proszę o rozwiązanie: i od wartości parametru m m∊ R a) 4* 2 ^Ix−1I = m b) 2^Ix−2I+x = m² wyniki znam bo są w odpowiedziach ale jak do tego dojść a) dla x< 0 ⇒ 2²*2^−x+1= 2^−x+3 dla x > 0 ⇒ 2²*2^x−1= 2^x+1 i czy teraz narysować wykres bo wyniki do a)1−równanie nie ma rozwiązania dla m ∊( −∞,4) − ma jedno rozwiązanie dla m=4 − ma dwa rozwiązania dla m ∊ (4 ,+ ∞ ) czy podobie rozwiązuje się b)

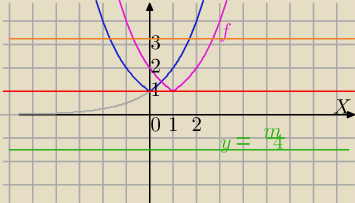
Mila: a) przekształcam lewą stronę aby łatwo było narysować wykres funkcji 4*2^|x−1|=m /:4

	m
2|x−1|=
	4

f(x)=2^|x−1| Rysujemy, po kolei: y=2^x→S_OY dla wykresu odpowiadającemu x≥0→y=2^|x| symetria tej części wykresu co po prawej stronie OY, następnie translacja o wektor [1,0] i otrzymujemy wykres f(x)=2^|x−1|

	m
1) Brak rozwiązań dla		<1⇔dla m<4
	4

	m
2) jedno rozwiązanie dla		⇔ dla m=4
	4

	m
3) dwa rozwiązania dla		>1⇔ dla m>4
	4

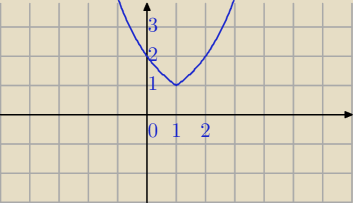
Mila: II sposób rysowania.( bez przekształceń) f(x)=2^|x−1| 1) |x−1|=x−1 dla x−1≥0⇔x≥1 wtedy masz wzór f(x)=2^x−1 i szkicujesz wykres dla x≥1, funkcja rosnąca 2)|x−1|=−x+1 dla x<1 wtedy:

	1
f(x)=2−x+1⇔f(x) =(		)x−1 funkcja malejąca dla x<1
	2

f(1)=1

proszę o rozwiązanie: dziękuję

Arek: Wyznacz zbiór wartości funkcji f(x)=x2−x+5 oraz jej osi symertii

Arek:

salamandra: f(x) = x²−x+5 a>0, więc ramiona paraboli w górę W(p,q) − wierzchołek

	−b
p =
	2a

	1
p =
	2

	1		1		1		3
q = f(p) = f(		) =		−		+ 5 = 4
	2		4		2		4

	3
zbiór wartości <4		; ∞ >
	4

	1
oś symetrii =x = p =
	2

Arek: Wyznacz, które wyrazy ciągu określonego wzorem an=−2(n−1)x(n−12) są niedodatnie

Arek: Help

Arek: Potrzebuje szybko

Arek: Naprawdę szybko