 , bo nie chcę dublować rozwiązań
, bo nie chcę dublować rozwiązań

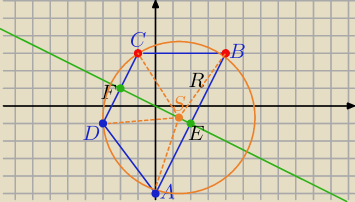 A(0,−5), D(−3,−1) AB : 2x−y−5=0 , EF : x+2y=0
DC ∥ AB i D∊DC ⇒ DC : 2(x−xD)−(y−yD)=0 ⇒ DC : 2x−y+5=0
Rozwiązując układ równań danych prostymi :
EF∩AB= {E} i EF∩DC={F}
rozwiąż te układy ........
otrzymasz E(2,−1) i F(−2,1)
punkty E i F są odpowiednio środkami podstaw AB i CD
( bo prosta EF jest osią symetrii tego trapezu
zatem:
xB=2xE−xA i yB=2yE−yA ⇒ .......... B(4,3)
xC=2xF−xD i yC=2yF−yD ⇒ ................ C(−1,3)
Okrąg opisany na trapezie ABCD jest okręgiem opisanym na trójkącie np: ABD
równanie okręgu : o : x2+y2−2ax−2by+c=0 , gdzie S(a,b) i r2=a2+b2−c >0
dla A(0,−5) 1/ 25 +10b+c=0 ⇒ c= −25 −10b
B(4,3) 2/ 16+9−8a−6b+c=0
D(−3,−1) 3/ 9 +1+6a+2b+c=0
A(0,−5), D(−3,−1) AB : 2x−y−5=0 , EF : x+2y=0
DC ∥ AB i D∊DC ⇒ DC : 2(x−xD)−(y−yD)=0 ⇒ DC : 2x−y+5=0
Rozwiązując układ równań danych prostymi :
EF∩AB= {E} i EF∩DC={F}
rozwiąż te układy ........
otrzymasz E(2,−1) i F(−2,1)
punkty E i F są odpowiednio środkami podstaw AB i CD
( bo prosta EF jest osią symetrii tego trapezu
zatem:
xB=2xE−xA i yB=2yE−yA ⇒ .......... B(4,3)
xC=2xF−xD i yC=2yF−yD ⇒ ................ C(−1,3)
Okrąg opisany na trapezie ABCD jest okręgiem opisanym na trójkącie np: ABD
równanie okręgu : o : x2+y2−2ax−2by+c=0 , gdzie S(a,b) i r2=a2+b2−c >0
dla A(0,−5) 1/ 25 +10b+c=0 ⇒ c= −25 −10b
B(4,3) 2/ 16+9−8a−6b+c=0
D(−3,−1) 3/ 9 +1+6a+2b+c=0
| 3 | 3 | 35 | ||||
rozwiąż ten układ równań otrzymasz; a= | , b= − | c= − | ||||
| 2 | 4 | 4 |
| 5 | ||
r2=..... = | √13 | |
| 4 |
