Geometria Blue: zad.1 Styczna do okręgu (x−2)² +(y−1)² =25, przecinająca oś OX w punkcie (9,0), może mieć równanie: A. 4x+3y−36=0 B. −4x+3y−36=0 C. 4x−3y−36=0 D.4x+3y+36=0 Nie wiem, czy był może jakiś wzorek na styczną do okręgu? Szczerze mówiąc średnio to pamiętam... Tylko nie bijcie, bo coś mi się wydaje, że to zadanie jest proste, tylko ja coś zapomniałam...

sushi_gg6397228: rysunek a potem uklad rownan −−> prosta i okrąg−−> musi wyjsc jedno rozwiazanie

Janek191: y = a x + b P = ( 9 ; 0) więc 0 = a*9 + b ⇒ b = −9 a y = a x − 9 a −−−−−−−−−−−−−−− Układ ( x − 2)² + ( y − 1)² = 25 y = a x − 9 a −−−−

Blue: Właśnie jak próbowałam liczyć tak, jak Janek , to mi zaczęły jakieś kosmiczne wyniki wychodzić... Cóż, może spróbuję jeszcze raz...

Blue:

	1		−5
Wyszło mi z tego układu a=		lub a=		, więc raczej coś źle... ale liczby normalnie
	4		6

kosmiczne.....

5-latek: Nie pisz o liczbach kosmicznych bo one rzadza światem

PW: Blue, nauka poszła w las? Metodą eliminacji. Jaki musi być współczynnik kierunkowy tej prostej? Dodatni, czy ujemny?

Blue: No właśnie nie wiem...

5-latek: A wiesz dlaczego nie wiesz ? Dlatego ze nie zrobilas rysunku i teraz sie domyslasz

PW: No to może inaczej: podstawiasz po chamsku (9, 0) do równań prostych − dwie z nich w ten sposób wyeliminujemy. Które?

Eta: S(2,1) , r= 5 odległość d punktu S od stycznej jest d=r=5 sprawdzamy , która z tych prostych przechodzi przez P(9,0) A/ 4x−3y−36=0 −−− pasuje i C/ 4x+3y−36=0 −−− też

	|4*2−3*1−36|
ale : dla A/ d=		≠ 5
	√25

	|4*2+3*1−36
dla C/ d=		= 5
	√25

zatem styczna ma równanie 4x+3y−36=0 odp; C/

daras: najłatwiej napisać że się właśnie tak liczyło jak mi koledzy podpowiadają ale...kosmiczne liczby wychodza albo UFO wylądowało i dawaj zasuwajcie dalej szanowni koledzy ja idę na

daras: albo Eta zmień kolor na blue

Eta: O co Ci chodzi daras ?

PW: Eta, to jest zadanie testowe. Kombinuję cały czas jak dojść do odpowiedzi nie licząc takich strasznych rzeczy jak d.

daras: nic personalnego Eta kocham Cię

Eta: PW ... chyba przesadzasz wyznaczanie odległości "d" ,to żadna "straszna rzecz" dla maturzysty ,który zdaje rozszerzenie ! daras ..... już dawno nikt mi nie wyznawał ....

daras: PW jest na dobrym tropie, skoro to test to trzeba po chamsku odwalać złe warianty

Eta: @daras czytałeś mój wpis 18:39

daras: 5−latek też dobrze kombinuje, bo jak sie już odwali 2 złe odp. i umie narysować pozostałe proste to się wylosuje prawidłowa wersję w ciągu 1,5 −2min i o to chodzi, nikt nie będzie przecież pytał dlaczego

daras: @Eta czytałem ale twój wywód jest za...długi gwoli wyjasnienia chodziło mi o zasady ja olewam ucznia, który nie rokuje czyli olewa moje nauki szkoda czasu chyba, że się robi sztukę dla sztuki dla własnej satysfakcji gorzej jak się przy tym zaniedbuje tych, którzy rokują

Blue: Po rozwiązaniu Ety już rozumiem. Dras gdybym kłamała, że tak ni liczę, to bym wyników, które mi wyszły nie podała

Eta: @Blue ..... i tak trzymaj

Blue: Ja nie uważam, że sposób Ety jest długi, właśnie prosty i klarowny, a Wy mi tutaj coś mieszacie z tym odrzucaniem odpowiedzi

PW: Przepraszam, więcej nie będę.

Blue: PW, nie o to mi chodziło Dzięki za pomoc i nie mów, że "więcej nie będziesz " Po prostu trochę się zdenerwowałam, bo Daras mnie wkurza! Ale Ciebie przepraszam i dzięki za pomoc, mimo że wolę rozwiązanie Ety

PW: Lubię Cię

daras: Eta & Blue

Blue: Nie czaje już sytuacji XD Daras dlaczego pocieszasz Etę?

Blue: A tak btw , to pewnie zamysł tego, kto układał to zadanie był taki jak Ety, bo zostawił już ładnie proste w postaci ogólnej

Eta:

daras: nie pocieszam tylko uważam, że jesteście zgraną parą

daras: prawidłową odpowiedzią jest oczywiście A @Eta przeczytałem ze zrozumieniem Twój wczorajszy wpis z 18:39 @PW jeden współczynnik kierunkowy będzie dodatni a drugi ujemny, bo styczne są dwie niestety 5−latek w swoim genialnym rozwiązaniu ich nie narysował ale rozgrzeszam go bo przecież jesteśmy w reżimie czasu rozwiązywania testu czyli ok. 1,5min/pytanie prawda? ale jeśli się wie jak te proste będą przebiegać, to się wybierze odpowiedź bez pudła! @Blue zapytałaś na wstępie czy jest jakiś wzorek na styczną do okręgu? Oczywiście, że jest wystarczy znaleźć współrzędne 2 wektorów P₁S i P₁P, P₁ − punkt styczności (należący do okręgu), P(9;0), S(2;1) te wektory są prostopadłe więc wystaczy sprawdzić ich iloczyn skalarny: P₁S◯P₁P = 0

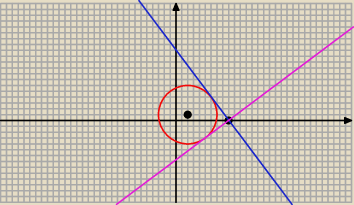
Janek191: ( x − 2)² + ( y − 1)² = 25 i A = ( 9; 0) więc S = ( 2; 1) r = 5 Równanie prostej stycznej do okręgu y = a x + b Ma przechodzić przez A = ( 9 ; 0) , to 0 = 9a + b ⇒ b = − 9a y = a x − 9 a lub w postaci ogólnej a x − y − 9a = 0 Odległość tej prostej od S =( 2; 1) jest równa r = 5 zatem

I 2a − 1*1 − 9a I
	= 5
√a2 + 1

I − 7a − 1 I = 5√a² + 1 I 7 a + 1 I = 5√a² + 1 7 a + 1 = 5 √a² + 1 lub 7a + 1 = − 5√a² + 1 49 a² + 14a + 1 = 25( a² + 1) 24 a² + 14 a − 24 = 0 12 a² + 7 a −12 = 0 Δ = 49 − 4*12*(−12) = 49 + 576 = 625 √Δ = 25

	− 7 − 25		4		− 7 + 25		3
a =		= −		lub a =		=
	24		3		24		4

zatem

	4		3		27
b = − 9* ( −		} = 12 lub b = − 9*(		) = −
	3		4		4

Mamy proste o równaniach:

	4		3		27
y = −		x + 12 lub y =		x −
	3		4		4

czyli 4 x + 3 y − 36 = 0 lub 3 x − 4 y − 27 = 0 ============== Odp. A ( niebieska prosta )

PW: Janek, zlituj się nad pacholęciem. Autorzy zadania zapewne mieli taki zamysł: 1.uczeń wyeliminuje dwie odpowiedzi − proste, które nie zawierają (9,0) 2. narysuje okrąg 3. narysuje dwie pozostałe proste i z rysunku odczyta, która jest styczna do okręgu. Podczas testu nie ma czasu na takie obliczenia. Podkreślam: pytanie nie brzmiało "Jakie jest równanie stycznej", lecz "Styczna (...) może mieć równanie"

Janek191: Dobrze, że odp. A jest prawidłowa. Gdyby D była prawidłowa, to też trochę trzeba policzyć − posprawdzać

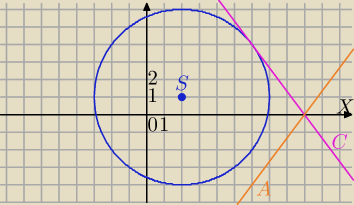
Mila: 1) sprawdzić które równania spełniają wsp. (9,0) 2) Następnie spróbować narysować okrąg i proste z punktu (A) i (C), jeśli da się ustalić jednoznacznie odp. to koniec zadania, jesli nie to obliczenia.

daras: Mila znowu odwrotnie A ↔ C

Mila: Tak, ma być z ujemnym wsp. kierunkowym. Dziekuję daras. Tu chodziło mi o metodę. Jednak Blue nie czyta juz tego wątku, może komuś się przyda.

daras: Blue może też by sie przydał, gdyby zabrała się za to zadanie sama