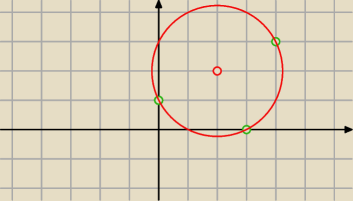
Geo. an. Blue: Do okręgu należą punkty : A= (0,1), B= (3,0) i C= (4,3). Wówczas: A. x²+y² −4x−4y−3=0 jest równaniem tego okręgu B. Promień tego okręgu ma długość 5 C. Środek okręgu ma współrzędne (2,2) D. okrąg przecina osie układu w punktach o całkowitych współrzędnych.. Narysowałam ten okrąg i mi tutaj pasuje odp. C i D

Tadeusz: ... to nie rysuj ... "i niech Ci nie podpada" − Napisz równanie okręgu znając trzy punkty na nim leżące −

Tadeusz:

PW: Blue, tradycyjnie postaram się podać najtrudniejsze z możliwych rozwiązanie, żeby pobudzić nietypowe myślenie. Gdyby podaną trójkę punktów A, B, C przesunąć o wektor [−2, −2], to otrzymalibyśmy punkty A' = (−2, −1), B' = (1, −2), C' = (2,1). Łatwo zauważyć, że punkty A' B', C' są jednakowo oddalone od początku układu współrzędnych − odległość od (0, 0) każdego z nich jest równa √4 + 1 =√5, czyli należą do okręgu o środku (0, 0) i promieniu √5. W ten sposób już wiemy jaki jest promień okręgu zawierającego A, B, i C − taki sam, bo przesunięcie nie zmienia promienia okręgu. Odpowiedź B wyeliminowana. Co jeszcze bardziej cieszy − środek okręgu zawierającego A, B, C uzyskamy przesuwając (0, 0) "z powrotem", czyli o wektor [2, 2]. Obraz (0, 0) w przesunięciu o wektor [2, 2} jest równy (2, 2) − zwyciężyła odpowiedź C pod warunkiem, że jest to test z jedną poprawną odpowiedzią. I nie pytaj "skąd ja miałabym być taka mądra, żeby wymyślić to przesunięcie". Parę przykładów i nabywa się tego spojrzenia. Często przesunięcie obiektu daje znakomite uproszczenie rachunków. W sekrecie zdradzę, że pewnie w ten sposób oni układają takie zadania − biorą coś prostego, o łatwym równaniu, i przesuwają dla utrudnienia rachunków.

Blue: PW, ale w odpowiedziach mam D

PW: To może się gdzieś pomyliłem? Sprawdźmy, niech (2, 2) = S. |SA| = √(0−2)² + (1−2)² = √4+1= √5 |SB| = √(3−2)² + (0−2)² = √1+4= √5 |SC| = √(4−2)² + (3−2)² = √4+1= √5. To teraz Ty sprawdź, czy odpowiedź D jest poprawna. Obawiam się, że to nie był test jednokrotnego wyboru (albo możliwość C to nie był punkt (2,2)).

Blue: PW to jest test jednokrotnego wyboru (aczkolwiek Aksjomat czasem robi błędy) i dobrze wszystko przepisałam... Ale powiedz mi dlaczego Ty odrzucasz odp. D Moim zadaniem i C i D są poprawne...

PW: No właśnie. Wcale nie odrzucam D. Zauważ, że pisałem o 14:13: zwyciężyła odpowiedź C pod warunkiem, że jest to test z jedną poprawną odpowiedzią. Widać przecież na rysunku Tadeusza, że D też jest poprawna, co łatwo sprawdzić rachunkowo rozwiązując równanie |(x,0) (2,2)| = √5 √(2−x)² + (2−0)²) = √5 − zarówno x=3 podana w zadaniu (pierwsza współrzędna punktu B) jak i ta druga, którą sprawdzamy, są całkowite. Podobnie dla punktów wspólnych okręgu z osią OY.

Blue: Czyli dobrze myślę, że odp C i D są poprawne

Blue: Pomoże ktoś z tym?

Kacper: Może ja?

Kacper: Odpowiedzi poprawne C i D

Blue: Czyli znów błąd w książce, ech, chyba złożę zażalenie

Kacper: A wg mnie autorzy chcieli specjalnie sprawdzić czy uczniowie myślą

Blue: Wątpię

daras: r = √5 ,( x_o,y_o) = (2;2), punkty przecięcia: x_i,y_i ∊{1; 3} => odp. C i D

daras: wyrzuć tę książkę albo spal odpowiedzi

Tadeusz: ... najłatwiej jeśli zauważysz, że trójkąt ABC jest prostokątny

	0−1		1
a1=		=−
	3−0		3

	3−0
a2=		=3
	4−3