Oblicz część pola koła o wierzchołku na trójkącie Grzegorz: Dany jest trójkąt równoboczny o boku 2 cm. Narysowano okręgi o środkach w wierzchołkach tego trójkąta i promieniu 1 cm. Oblicz pole części trójkąta ograniczoną łukami tych okręgów (do 0,01). Odp: 0,16 cm. Ale nie wiem jak to obliczyć. Liczę tak. Pole koła to: πr² = 3,14 * 1 cm = 3,14 cm². Trójkąt równoboczny ma każdy kąt 60 stopni. Ponieważ środek koła jest na wierzchołku, to całe pole trójkąta, ograniczone łukiem pokrywa się z częścią koła, w oparciu o kąt wpisany na wierzchołku o 60 stopniach. Kąt 60 stopnia to 1/6 całego koła (poprzez 60/360 = 1/6), zatem w mojej ocenie 1/6 pola koła pokrywa trójkąt. Czyli 1/6 * 3.14 = 0,73 cm², ale to jest wynik za duży nawet na 3 łuki...

sushi_gg6397228: zrób rysunek

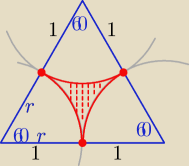Eta: P= P(Δrównobocznego) − 3*P(wycinka koła)

	1
PΔ=....= √3 Pw=		πr2 , r=1
	6

P= ............ ≈ 0,16

Grzegorz: Nie wiem, ale mimo podanego wzoru coś mi nie wychodzi. Pole trójkąta = √3 = 1,44

	1
Pw=		πr2 = 0,16 * 3,14 * 12 = 0,52 cm2
	6

3*P = 1,56 P= P(Δrównobocznego) − 3*P(wycinka koła) = 1,44 − 1,56 Co pomieszałem?

Eta: √3≈ 1.73

Eta:

	1
3*Pw= 3*		π= 0,5*3,14≈1,57
	6

1,73−1,57=...........

Grzegorz: Dziękuję, uprzejmie. Dobrej nocy.