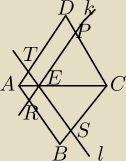
. Pi: W rombie ABCD wybrano na przekątnej AC punkt E. Przez punkt E poprowadzono prostą k równoległą do boku AD, przecinającą boki AB i CD odpowiednio w punktach R i P, oraz prostą l równoległą do boku AB, przecinającą boki AD i BC odpowiednio w punktach T i S (zobacz rysunek obok). Wykaż, że suma obwodów czworokątów RBSE i TEPD jest równa obwodowi rombu ABCD.

pigor: ..., np. tak : z warunków zadania i własności rombu : Ob._RBSE+Ob._TEPD= 2(|RB|+|BS|) + 2(|TD|+|DP|)= = 2(|RB|+|AR| + |TD|+|AT|)= 2(|AB| + |AD|)= Ob._ABCD c.n.w.

Pi: Bardzo dziękuję