Jaka długość może mieć
Ewka : 1.Jaka długość może mieć odcinek AB jeśli :
a) |AC| =5 i |BC| = 3
b) l AC| = 1 i l BC| = 4
c) | AC| = 3 i |BC| = 3
Rozwiąz rozne przypadki położenia punktów A,B, C
2. Jaka figurą jest zbiór wszystkich punktów P płaszczyzny, dla których :
a) | OP| < r ,
b) |OP| > r
gdzie O jest ustalonym punktem płaszczyzny a r − liczbą dodatnią
Prosze o pomoc

6 wrz 15:05
PW: A po co trzy razy zamieszczasz tę prośbę?
6 wrz 15:18
Ewka : możliwe że winna mojego laptopa czasami cos sie mu zdarzy kilkakrotnie powtórzyć
6 wrz 15:20
Ewka : może jesteś w stanie mi pomóc ?
6 wrz 15:22
Ewka : Pomoże ktoś?
6 wrz 15:27
Ewka : pomoże ktos?
6 wrz 15:37
sushi_gg6397228:
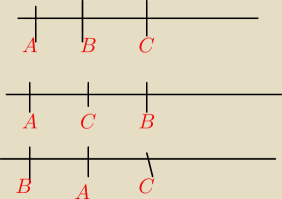
6 wrz 15:52
Ewa: nic mi to nie mówi
6 wrz 15:53
sushi_gg6397228:
a) masz podane |AC|=5 to sobie zaznaczasz kredka dlugosc i wpisujesz liczbe 5
zaznaczasz |BC| i wpisujesz liczbę 3
a potem masz dodawanie i odejmowanie w zakresie do "10"
6 wrz 15:59
sushi_gg6397228:
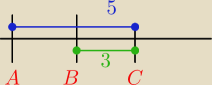
wie ile jest miedzy "A" i "B"
6 wrz 16:01
Ewa: i tak wszytsko
6 wrz 16:02
sushi_gg6397228:
masz tylko 3 warianty na każdy podpunkt
6 wrz 16:04
sushi_gg6397228:
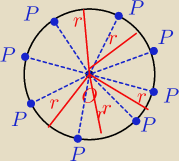
masz rysunek do zadania numer 2− pomyśl
6 wrz 16:07
Ewa: jestem glupia nie wymysle
6 wrz 16:16
PW: Ewka, nie określiłaś, czy punkty A, B, C należą do płaszczyzny, czy tylko do prostej.
Jeżeli do płaszczyzny, to sugestie sushi są niewystarczające − trzeba się powołać na
nierówność trójkąta i wniosek z niej, brzmiące: dla dowolnych trzech punktów płaszczyzny
odległość dwóch z nich jest nie mniejsza od różnicy i nie większa od sumy odległości dwóch
pozostałych. Przy oznaczeniach jednoliterowych dla długości odcinków:
b−a ≤ c ≤ a+b
− przyjmujemy tradycyjne oznaczenia a = |BC|, b = |AC|, c = |AB|.
6 wrz 17:56


 wie ile jest miedzy "A" i "B"
wie ile jest miedzy "A" i "B"
 masz rysunek do zadania numer 2− pomyśl
masz rysunek do zadania numer 2− pomyśl