całka podwójna papaja: Prosze o pomoc w rozwiązaniu zadania z analizy(całki podwójne). Oblicz pole powierzchni ograniczonej x²+y²≤2*x i x²+y²≤2*y . Przecinają się tu dwa okręgi i najbardziej mnie zastanawia czy powinnam tu po prostu przyjąć obszar 0≤x≤1 −√4−x²≤y≤√2*x−x²+2 i męczyć się z całkami funkcji niewymiernych czy może podzielić ten obszar na dwie części i zmienić współrzędne na biegunowe(nie wiem czy w tym przypadku można)? bardzo proszę o pomoc

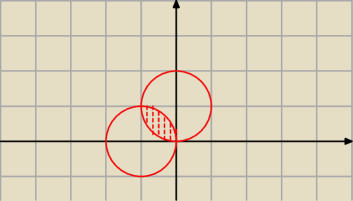
MQ: Ja bym to zamienił na wsp. biegunowe, bo dostajesz taki oto obszar, jak na rysunku, a wsp. biegumowe masz w granicach:

π
	≤ φ ≤ π
2

oraz:

	π		3π
0 ≤ r ≤ −2cosφ dla		≤ φ ≤
	2		4

	3π
0 ≤ r ≤ 2sinφ dla		≤ φ ≤ π
	4

Dostajesz w sumie dwie proste całki. Nie zapomnij oczywiście o jakobianie.

papaja: Bardzo dziękuję za pomoc!