Prośba o pomoc w rozwiązaniu tych dwóch przykładów Szakal: Znaleźć przedziały monotoniczności funkcji f(x) x³/3−x² Znaleźć ekstremum funkcji : f(x) √^1−x_1+x

Kacper: teoria...

Ajtek: Mamy gdzieś moderatora?

Godzio:

Ajtek: Cześć Godzio, miło, że wpadłeś

Janek191:

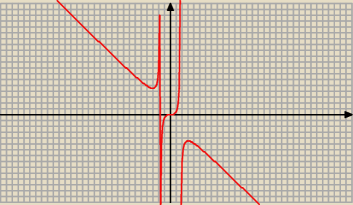
	x3
f(x) =		x ∊ ℛ \ { −√3, √3 }
	3 − x2

więc pochodna

	3 x2*( 3 − x2) − x3*( − 2x)		9 x2 − x4
f '(x) =		=		=
	( 3 − x2)2		( 3 − x2)2

	x2*( 9 − x2)		x2*( 3 − x)*( 3 + x)
=		=		= 0 ⇔
	(3 − x2)2		( 3 − x2)2

⇔ x = 0 lub x = − 3 lub x = 3 oraz f '(x) > 0 ⇔ x ∊ ( − 3 ; 3 ) \ { − √3 ,0, √3 } więc funkcja f rośnie w przedziałach : ( − 3; −√3) , ( − √3; √3 ), ( √3; 3 ) a maleje w przedziałach : ( − ∞ ; − 3) , ( 3 ; + ∞).