f.^2 rysunek: szkicujac wykresy odpowiednich funkcji rozwiaz nierownosc Ix²−6 xI<=2x algebraicznie wychodzi mi poprawnie, jednak nie potrafię zrobić rysunkiem odp. xe <4,8> u {0}

Eta: 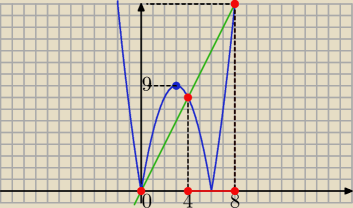y=2x y=|x²−6x|

pigor: ..., rysujesz parabolę f(x)= x²−6x= x(x−6) i p=−3 i f(3)= −9=q i odbijasz jej część spod osi Ox symetrycznie względem niej, teraz rysujesz prostą y=2x, która przecina ten wykres w dwóch punktach jak widzisz o x>0 będących rozwiązaniem równania : |x²−6x|=2x ⇔ x²−6x= 2x v x²−6x= −2x ⇔ (x²= 8x v x²= 2x) i x>0 ⇔ ⇔ x=8 v x=2 stąd i z wykresu odczytujesz , zedana nierówność |x²−6x|≤ 2x ⇔ x∊ [2;8] − szukany zbiór rozwiązań co możesz ładnie na osi Ox zaznaczyć np. kolorem . ...

pigor: ..., no tak , znów ... za długo się bawiłem, masz już to na wykresie.

Eta: π.. ⇔x²=8x v x²= 4x

rysunek: 2³ =8 więc czemu dla argumentu 2 funkcja przyjmuje wartość 9 ?

Eta:

	6
xw=		=3
	2

y_w=f(3)=\ 3²−6*3\= |−9 |=9 to wierzchołek paraboli W(3,9)

pigor: ... hmm; dzięki η, w głowie było co innego; przepraszam cóż zaczyna się ... noc; czas na tenis dziewczyn na usopen. ...

rysunek: a skad wiadomo ze Ix²−6i dla argumentu 8 przyjmuje wartosc 16?

Eta: f(8)=|8²−6*8|=............