Proszę o pomoc Avenu: Oblicz pole figury ograniczonej krzywymi x−y+1=0 y²+2x−1=0 Treść zadania z któym nie moge sobie poradzic, jeśli ktoś byłby na tyle miły i mogłby mi pomoc w tym, potrzebuje je bardzo gdyz bd na poprawce

sushi_gg6397228: najpierw zrób rysunek

Avenu:

Avenu:

Avenu: nie wiem czy dobrze to wykreslilem

sushi_gg6397228:

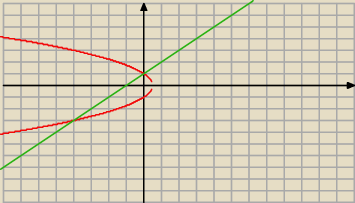
5-latek: Post 20:23 A ja sie zastanawialem jak wygladal exkalibur Nie wiem czy dobrze mysle ale jesli dobrze to x−y+1=0? wiec y=x+1 Teraz masz postac y²+2x−1=0 to y²=−2x+1 to y= √−2x+1 Taki w tym programie wyszly te wykresy tych funkcji Teraz musisz zanalezc pukty preciecia tych wykresow czyli √−2x+1=x+1 dla −2x+1>=0 i dla x+1>=0 i wyznacz czesc wspolna obu warunkow Dla tych warunkow masz obie strony rownania nieujemne wiec mozesz podniesc je do kwadratu czyli −2x+1=(x+2)² i to sobie rozwiaz Co do calki to wybacz ale nie pomoge

5-latek: Przepraszam ale jednak zle wykres y²+2x−1=0 zrobilem i takze przeksztalcenie

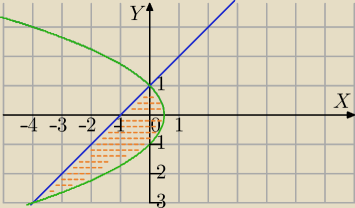Mila: x−y+1=0 , y²+2x−1=0 y=x+1 y²=−2x+1 y=√−2x+1, −2x+1≥0 lub y=−√−2x+1, −2x+1≥0 Wsp. wierzchołka paraboli

	1
x=		,y=0
	2

Punkty przeciecia ( umiesz obliczyć?) (−4,−3) (0,1) Obszar jest normalny wzgledem osi OY −3≤y≤1

	−1		1
x=y−1 i x=		y2+
	2		2

	−1		1		−1		3
P=−3∫1[(		y2+		)−(y−1) ]dy=−3∫1(		y2−y+		) dx=
	2		2		2		2

	1		1		3
=[−		y3−		y2+		y]−31=... licz sama
	6		2		2

	32		16
=		=
	6		3

II sposób 3 obszary normalne względem OX.− trochę więcej rachunków P=2*₀∫^1₂(√−2x+1 dx+₍₋₄₎∫⁰ (x+1−(−√−2x+1) dx= =

5-latek: Dobry wieczor Milu pozdrawiam czyli braklo mi jeszcze y=−√−2x+1 Zapomnialem calkiem o tym

Mila: Witam