Planimetria 2 Blue: Jeszcze trochę zadań z planimetrii: zad.1 Bok rombu ABCD ma długość 18, a promień okręgu wpisanego w ten romb a długość 4,5. Miara kąta ABD jest równa: A. 30 B. 45 C. 60 D.75 Mi wyszło A, bo rozumiem to tak, że h=9, ale w odp mam D. Dlaczego zad.2 Wewnątrz trójkąta równobocznego o boku długości 100√3 wybrano punkt K taki, że jego odległości od dwóch boków trójkąta są równe 19 i 8. Oblicz odległość punktu K od trzeciego boku. Zakoduj cyfry setek, dziesiątek i jedności otrzymanego wyniku. zad.3 W rombie ABCD, w którym bok ma długość 9 i kąt przy wierzchołku A =60, poprowadzono odcinek AE, dzielące (chyba tutaj powinno być dzielący ) romb na trzy figury o równych polach. Oblicz długość odcinka AE. Zakoduj trzy początkowe cyfry po przecinku rozwinięcia dziesiętnego liczby |AE|. Bardzoooo proszę o pomoc w tych zadankach Będę Wam bardzo wdzięczna za odpowiedzi

Mila: 1) obliczyłaś miarę kata ostrego: ∡A=30⇒ ∡B=180−30=150 Połowa kąta B to 75⁰. Popracuj nad wskazówkami, teraz muszę zrobić przerwę.

Godzio: Chcesz wskazówki czy rozwiązania?

pigor: ..., np. zad.2. z warunków zadania tak : niech x=? − szukana o, to odległość punktu K od trzeciego boku Δ, to suma pól "małych ΔΔ'' równa polu całego Δ równobocznego : czyli ¹₂*100√3 (x+8+19)= ¹₄(100²*3)√3 /*0,04/√3 ⇔ ⇔ 2(x+27)= 100*3 ⇔ x+27= 150 ⇔ x= 123 ... i tyle ... −−−−−−−−−−−−−−−−−−−−−− ..., no to w kratki na arkuszu maturalnym wpisujesz następujące cyfry : w pierwszą kratkę (to cyfra setek) wpisujesz cyfrę 1 liczby 123 (wyniku) w drugą kratkę (cyfra dziesiątek) 2 i w trzecią cyfrę jedności 3 . ..

daras: to prawie jak w Totto Lotku, chyba nie zdałbym juz matury

Blue: W tym pierwszym to ja chyba źle przeczytałam i zły kąt obliczyłam, teraz widzę hhaha

Blue: Pigor wszystko rozumiem ^^ Jesteś geniuszem, niby zadanko aż takie trudne nie jest, ale najpierw trzeba zauważyć te trójkąty, których ja nie dostrzegałam

Blue: Daras mi się też nieszczególnie podoba to kodowanie odp., ale co zrobić

Blue: Czekam teraz na rozwiązanie trzeciego, bardzo proszę

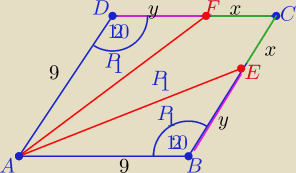Eta: Blue myślę,że w zad3/ powinno być ,że odcinki |AE|=|AF| −− dzielą romb na trzy części o równych polach

	1
P(ΔABE)=P(ΔAFD)=		P(rombu)
	3

1		1
	P(rombu)=		*9*9*sin60o=....
3		3

	1
P(ΔABE)=		*9*y*sin120o=....
	2

porównaj te pola i wyznacz y=... z tw. kosinusów w ΔABE wyznacz |AE|=....

pigor: ... cieszę, że mój gotowiec uczy ... myśleć, a jaka radość jak się go rozszyfruje (zrozumie), prawda

Eta: π..

Ben Akiba: a mi się nie podoba, że {P{blue]] ciągle tylko" czeka na rozwiązanie zadania" może powinnaś przeczytać Lilavati ?

pigor: ... moje gotowce to właśnie takie zagadki, a co do Lilavati pana Jeleńskiego, to kto teraz by czytał taką piękną książkę, jak komputer stoi i czeka ... obok

Blue: Eta dziękuję Ci To zadanie właśnie wydawało mi się niekompletne i pewnie dlatego nie potrafiłam się nawet za nie wziąć xd Ach ten Aksjomat... a mój nauczyciel niby tak chwali to wydawnictwo..

Blue: Eta, wynik się zgadza

Eta: