aksjomat Bulgotek: 1. W ostrosłupie prawidłowym trójkątnym krawędź boczna jest trzy razy dłuższa od krawędzi podstawy Oblicz cosinus kąta zawartego między ścianami bocznymi tego ostrosłupa. ODP cos alfa=³⁹₇₀ 2.Objętość graniastosłupa prawidłowego czworokątnego jest równa 16, a pole jego powierzchni bocznej jest równe 32. Oblicz cosinus kąta utworzonego przez przekątne ścian bocznych wychodzące z tego samego wierzchołka graniastosłupa ODP cos alfa =⁴₅ 3. Punkty A=(1,4) i B=(5,2) są kolejnymi wierzchołkami prostokąta o polu 30. Wyznacz współrzędne pozostałych wierzchołków tego prostokąta wiedząc, że leży on w pierwszej ćwiare układu współrzędnych. ODP

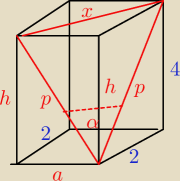
Janek191: z.2 Mamy V = a² *h = 16 P_b = 4a*h = 32 więc

a2 h		16		1
	=		=
4a*h		32		2

a		1
	=		⇒ a = 2
4		2

4*2*h = 32 ⇒ 8 h = 32 ⇒ h = 4 x = a√2 = 2√2 ⇒ x² = 4*2 = 8 p² = 2² + 4² = 4 + 16 = 20 Z tw. cosinusów mamy x² = p² + p² − 2 p*p cos α 8 = 20 + 20 − 2*20 cos α 40 cos α = 32

	32		4
cos α =		=
	40		5

======================

Janek191:

	34		17
Mnie też w z. 1 wyszło cos α =		=
	70		35

AF ⊥ BF

Mila: Dziekuję Janek za poprawkę; do wpisu 22:44 AF⊥SB CF⊥SB Gdy pisze się zależności, to czasem ucieka do góry rysunek.

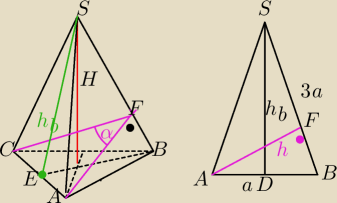Mila: Scisny boczne sa przystającymi trójkatami równoramiennymi: AF⊥SB i CF⊥SB α− kat między ścianami bocznymi

	1
PΔABS=		*a*hb
	2

W ΔSDB:

	1
(3a)2=(		a)2+(hb)2
	2

	35		a√35
hb2=		a2 stad hb=
	4		2

	1		a√35
PΔABS=		*a*		⇔
	2		2

	a2√35
PΔABS=
	4

Pole tego trójkąta możemy obliczyć drugim sposobem

	1
PΔABS=		*3a*h
	2

1		a2√35
	*3a*h=
2		4

	a√35
stąd h=
	6

W ΔCAF z tw. cosinusów mamy:

	a√35		a√35		a√35		a√35
a2=(		)2+(		)2−2*(		)*(		)*cosα⇔
	6		6		6		6

	35		35		35
a2=		a2+		a2−2*		a2*cosα
	36		36		36

	70		70
a2=		a2−		a2*cosα /:a2,
	36		36

34		70
	=		*cosα
36		36

	34		17
cosα=		=
	36		35

==============

Mila: Poprawka ostatniej linijki 23:58

	34
cosα=		⇔
	70

	17
cosα=
	35

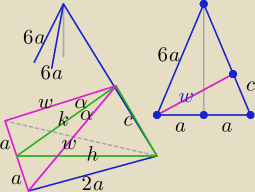Bogdan: Zadanie 1. Można rozwiązać także w ten sposób:

	a		c		a
h = a√3,		=		⇒ c =		,
	6a		2a		3

	26
k2 = h2 − c2 = 3a2 − c2 =		a2
	9

	k2		2k2−k2−a2		k2 − a2
cos2α = 2cos2α−1 = 2*		− 1 =		=		=
	w2		k2+a2		k2 + a2

	26   a2 − a2 9		17a2		17
=		=		=
	26   a2 + a2 9		35a2		35

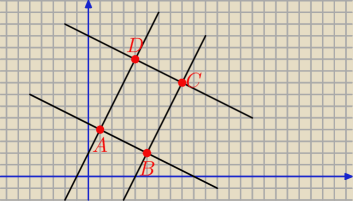Bogdan: Zadanie 3. A = (1, 4), B = (5, 2), C = (x_C, y_C), D = (c_D, y_D), x_c, y_C, x_D, y_D > 0

	1
prosta AB: y = a1x + b1, a1 = −
	2

prosta BD: y = a₂x + b₂, prosta AD: y = a₃x + b₃, a₂ = a₃ = 2 |AB| = √20 = 2√5, 2√5*|BC| = 30 ⇒ |BC| = |AD| = 3√5

	yC − 2
a2 =		= 2 ⇒ (yC − 2) = 2(xC − 5) ⇒ yC = 2(xC − 5) + 2
	xC − 5

|BC|² = (x_C − 5)² + (y_C − 2)² ⇒ 45 = (x_C − 5)² + 4(x_C − 2)² ⇒ (x_C − 5)² = 9 x_C − 5 = 3 lub x_C − 5 = −3 ⇒ x_C = 8 i y_C = 8 lub x_C = 2 i y_C = −4 C = (8, 8), C = (2, −4) odrzucamy.

	yD − 4
Analogicznie obliczmy współrzędne punktu D: a3 =		= 2 ⇒ (yD − 4) = ...
	xD − 1

i |AD|² = (x_D − 1)² + (y_D − 4)² itd.

Eta: Widzę chochlika prosta BC : y=a₂x+b₂