funkcja Adam: Naszkicuj wykres funkcji f:R−>R, jeśli wiadomo, że f'(x)=0 dla x∊(−∞;0) f'(2)=0,f''(x)>0 dla x∊(0,2) oraz f''(x)<0 dla x∊(2;+∞) Ma ktoś pomysł jak to będzie wyglądało ?

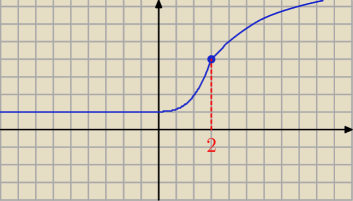
Godzio: Na przykład tak: f'(x) = 0 dla x ∊ (−∞,0) −− z tego wynika, że w tym przedziale funkcja jest stała f'(2) = 0 + f''(x) > 0 + f''(x) < 0 w odpowiednich przedziałach ⇒ 2 jest punktem przegięcia

Adam: No właśnie nie rozumiem, dlaczego w tym przypadku jest funkcja stała . Da się to jakoś wyjaśnić?

J: Jeżeli f(x) = k ( funkcja stała), to f'(x) = 0

Adam: No dobra, ale jak uzasadnić, że istnieje punkt przegięcia. Napisać, że funkcja zmienia znak przy przejściu przez punkt x=2 ?

J: nie... w tym pnkcie f'(x) = 0 i druga pochodna zmienia znak

asd: Ale jak to pkt przegięcia jest w 0 ? Skoro w 2 zmienia druga pochodna znak ?

asd: up

asd: up

Adam: up

Godzio: Skąd 0 wziąłeś?

Adam: No bo szczerze, dlaczego nie można zapisać, że w funkcja ma w punkcie x=2 punkt przegięcia tylko w f'(x)=0

Godzio: Przecież cały czas jest mówione, że w punkcie x = 2 ma punkt przegięcia, bo druga pochodna zmienia tam znak.

Adam: Spoko, kumam