 hej. Czy potrafiłby ktoś pomóc w takim zadanku z planimetrii:
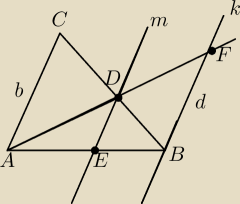
Dany jest trójkąt ABC, w którym |AC| = b. Prze wierzchołek B poprowadzono prostą k równoległą
do AC, a prze punkt D ∊ BC poprowadzono prostą m również równoległą do AC i przecinającą bok
AB w punkcie E. Prosta AD przecina prostą k w punkcie F. Oblicz |DE| wiedząc, że |FB| = d.
hej. Czy potrafiłby ktoś pomóc w takim zadanku z planimetrii:
Dany jest trójkąt ABC, w którym |AC| = b. Prze wierzchołek B poprowadzono prostą k równoległą
do AC, a prze punkt D ∊ BC poprowadzono prostą m również równoległą do AC i przecinającą bok
AB w punkcie E. Prosta AD przecina prostą k w punkcie F. Oblicz |DE| wiedząc, że |FB| = d.
| d | |AB| | x | |AB|−|AE| | |||||
(*) | = | i | = | i mnożąc stronami ⇒ | ||||
| x | |AE| | b | |AB| |
| d | |AB| | |AB| | d | |||||
⇒ | = | −1 ⇒ | = | +1, to stąd i (*) | ||||
| b | |AE| | |AE| | b |
| d | d | d | d+b | bd | |||||
= | +1 ⇔ | = | ⇔ x= | . ...  | |||||
| x | b | x | b | b+d |

| d | |AB| | x | |AB|−|AE| | |AE| | |||||
= | i | = | = 1− | ||||||
| x | |AE| | b | |AB| | |AB| |
| x | x | x | d−x | ||||
=1− | ⇒ | = | ⇒xd=bd−bx ⇒ xd+xb=bd | ||||
| b | d | b | d |
| bd | ||
x(b+d)=bd ⇒x= | ||
| b+d |

