najwieksza i najmniejsza wartosc funkcji licznowej Dawid: Pomocy, kompletnie niewiem jak "ugryźc" to zadanie z "dwiazdka" wykaż że funkcja określona

	x
wzorem f(x)=		x∊R, przyjmuje najmniejszą wartość rowna −1/2 zas najwieksza 1/2
	1+x2

Dawid: czy macie jakis pomysł?

Kacper: oczywiście

x
	=a, a− parametr
1+x2

Zbadaj dla jakiej wartości parametru a równanie ma rozwiązanie

Eta:

	x
y=		/*(1+x2) , D=R
	1+x2

y(1+x²)=x

	1		1
yx2−x+y=0 Δ =1−4y2≥0 ⇒ (1−2y)(1+2y) ≥0 ⇒ y∊<−		,		>
	2		2

	1		1
ZW= <−		,		>
	2		2

	1		1
zatem ymin= −		, ymax=
	2		2

c.n.w

ICSP: mamy : −(x+1)² ≤ 0 ≤ (x−1)² −x² −2x − 1 ≤ 0 ≤ x² − 2x + 1 // + 2x −(x² + 1) ≤ 2x ≤ (x² + 1) // : x² + 1 > 0

	2x
−1 ≤		≤ 1// : 2
	x2 + 1

	1		1
−		≤ f(x) ≤
	2		2

	1		1
Dodatkowo z pierwszej równości widać, ze f(1) =		oraz, że f(−1) = −
	2		2

c.n.p.

Dawid: tzn niemialem jeszcze nic o parametrach w takich rownaniach...

Dawid: dziekuje bardzo

Eta: "CPN"

ICSP:

Eta:

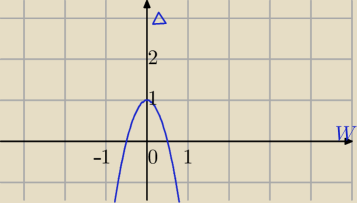
Mila: w− wartość funkcji

x
	=w
1+x2

x=w*(1+x²)⇔w*x²−x+w=0 sprawdzimy dla jakiego w to równanie ma rozwiązanie. 1) w=0 wtedy mamy równanie : −x=0, x=0 rownanie ma jedno rozwiązanie. 2)w ≠0 Δ=1−4w² Aby równanie miało rozwiązanie musi byc spełniony warunek: Δ≥0⇔ 1−4w²≥0⇔(1−2w)*(1+2w)≥0

	1		1
⇔w∊<−		,		>
	2		2

PW: Jak się bawić, to się bawić

	1
f(x) =		, x∊R\{0}.
	1   +x x

Dla x>0 znana jest nierówność

	1
x+		≥ 2,
	x

a więc dla takich x odwrotności spełniają nierówność

	1		1
		≤		.
	1   +x x		2

A jak to jest dla x<0? (nie tłumaczcie mi, ale adepci niech pomyślą).

pigor: ..., coś mi się zdaje, że .... nie wymyślą , ale jestem gotów podpowiedzieć jak ktoś z nich .. ładnie poprosi . ..

Eta: