Trzeba znaleźć zbiór wartości funkcji takiej. Marek: Trzeba znaleźć zbiór wartości funkcji. Prosiłbym o dokładne wytłumaczenie co i jak, bo nie ogarniam; hehe

	7
f(x) =
	sin2x − sinx − 12

daras: ale mam nadzieję, że ogarniasz w jakich granicach zmienia się sinus? ewentualnie jesteś w stanie to wyguglac?

Marek: pomoże ktoś please −.−

J:

	7
f(x) =		, podstaw: t = sinx i zobacz ,jak zachowyje się funkcja:
	(sinx−4)(sinx+3)

	7
f(x) =		w przedziale <−1,1>
	(t−4)(t+3)

Ben Akiba: właśnie dostałeś wskazówkę i co zrobiłeś ?

Marek:

	−7		−4
Już wiem − wyjdzie Zwf=<		,		>
	10		7

Marek: dzięki ziomeczki, pozdro

J: Może prościej ... funkcja sinx przyjmuje tylko wartości z przedziału <−1,1> oraz

	7
mianownik nie zeruje się w przedziale <−1,1> , zatem dla funkcji
	t2 − t −12

policz f(−1) oraz f(1) i to bedzie zbiór wartości f(x)

J: Przedział zły ...

Marek:

	−7		−7
zwf: <		,		> TERAZ JEST NA PEWNO DOBRZE!
	10		12

john2:

	−7		−4
Marek, jak doszedłeś do wyniku <		,		>?, bo wg wolframa tak ma właśnie być:
	10		7

http://www.wolframalpha.com/input/?i=range+f%28x%29%3D7%2F%28sin^2x+-+sinx+-12%29

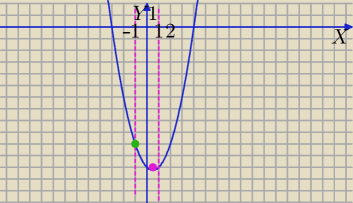Mila: Z rysunkiem: g(t)=t²−t−12, t∊<−1,1>

	1
tw=		∊<−1,1>
	2

	1		−49		1		4
g(		)=		wartość najmniejsza g(t) ⇔f(		)=−		wartość największa f(x)
	2		4		2		7

	−7
g(−1)=−10 wartość najwięsza g(t) w przedziale <−1,1>⇔f(−1)=		wartość najmniejsza f(x)
	10

	−7		4
y∊<		,−		>
	10		7

john2: Dziękuję.

Mila:

daras: @john2 Marek po prostu strzelał hehe