rozwiązywnaie trójk. prostokątnych seb4: W równoległoboku ABCD dane są: długość boku |AB|=5√3, długość przekątnej |AC| = 12 oraz kąt azawarty między bokiem AB a przekątną AC ∡CAB=30*. Oblicz miary kątów równoległoboku.

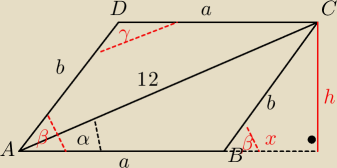
Janek191: α = 30^o I AB I = 5√3 = a I AC I = 12 Mamy

h		1
	= sin α = sin 30o =
12		2

więc h = 6 ( a + x)² + h² = 12² ⇒ ( a + x)² = 144 − 6² = 108 = 36*3 więc a + x = √36*3 = 6√3 czyli 5√3 + x = 6√3 x = √3 dlatego

	h		6
tg β =		=		= 2√3 ≈ 3,4641
	x		√3

β ≈ 74^o γ ≈ 180^o − β ≈ 116^o

Janek191: Pomyłka − miało być : β ≈ 74^o γ ≈ 106^o ===========