funkcja kwadratowa
Ania@: funkcja kwadratowa f przyjmuje największą wartość równą 315, a zbiorem rozwiązań
nierówności f(x)>0 jest przedział (−5,3). wyznacz wzór funkcji f w postaci ogólnej.
9 lis 21:49
Nikka: Funkcja kwadratowa y=f(x)=ax[2}+bx+c ma przyjmuje wartość największą w yw = − Δ4a,
yw − współrzędna y wierzchołka paraboli
Stąd
− Δ4a = − b2−4ac4a = ... (nie mam pewności czy jest tam jedna trzecia czy jedna
piąta)
f(x)>0 dla x∊(−5,3) czyli liczby −5 i 3 są pierwiastkami funkcji
f(−5)=0
f(3)=0
− b2−4ac4a =...
25a−5b+c=0
9a+3b+c=0
dostajemy układ trzech równań, z którego obliczamy a, b, c
9 lis 22:08
Aza:
Podam prostszy sposób

z rozwiązania nierówności widać ,że
x
1= −5 v x
2 = 3 i a <0 ,bo ramiona paraboli do dołu
zatem:
| | x1+x2 | | −5+3 | |
xw = |
| = |
| = −1
|
| | 2 | | 2 | |
wiemy ,że f(−1)= 3
15
korzystamy z postaci iloczynowej:
f(x) =
a( x+5)(x −3) podstawiając za x = −1 i f(−1) = 3
15
wyznaczamy
a
a( −1+5)(−1−3)= 3
15
a* (−16)=
165 =>
a= −15
teraz już prosto:
f(x) = −
15(x +5)(x −3) = −
15( x
2 +2x −15) = −
15x
2 −
25x +3
odp:
f(x) = −15x2 −25x +3
10 lis 01:07
Godzio: o to tego to nie jestem pewien czy bym zrobił bo dzisiaj mieliśmy pierwszy temat z funkcji
kwadratowej

tzn Δ , wspolrzedne wektora i postac iloczynową po dzisiejszej lekcji mysle ze
bym juz zrobil

10 lis 01:21
Godzio: czekaj ja bym tak zrobił:
10 lis 01:26
Godzio:
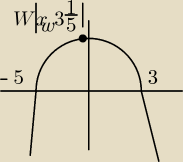
i dziś tez się dowiedziałem że x
w można z tych dwóch pkt −5, 3
cztli bym to podstawil do wzoru f
i wiem ze przechodzi przez te 2 pkt czyli czyli bym zrobil chyba układ równań
0=9a+3b+c
0=25a+5b+c
ale nie wiem czy to dobrze by było
10 lis 01:30
Godzio: pierwszy powinien byc
10 lis 01:34
Godzio: o i tak samo 3 bo x=−5
0=9a+3b+c
0=25a−5b+c
10 lis 01:36
Aza:
ale po co liczyć układ z a ,b, c
skoro wiesz ,że f(x
w) = y
w i znasz miejsca zerowe
to pisząc postać iloczynową masz prościej!
f(x) = a ( x +5)(x −3)
i masz tylko jedną niewiadomą "a"
bo wiesz ,ze f( −1) = 3u{1}{5]
itd......... o wiele tak łatwiej

co nie znaczy ,że ten Twój i
Nikki sposób jest błędny ( poprawny jak
najbardziej)
Na maturze czas jest [C{drogocenny]] ,
stąd należy wybierać najkrótszą drogę ( jak w życiu........
Pora

Dobrej nocy
Godzio 
... do jutra ....
10 lis 01:56
Godzio: Dobranoc

10 lis 02:03
Nikka: 
to była pierwsza myśl... zgadzam się, że czas na maturze jest drogocenny

Aza przy okazji Twojego rozwiązania też się czegoś nauczyłam − zauważyłam, że a<0, ale
brakowało mi trzeciego równania (tego z x
w)

10 lis 07:37
 z rozwiązania nierówności widać ,że
x1= −5 v x2 = 3 i a <0 ,bo ramiona paraboli do dołu
zatem:
z rozwiązania nierówności widać ,że
x1= −5 v x2 = 3 i a <0 ,bo ramiona paraboli do dołu
zatem:
 tzn Δ , wspolrzedne wektora i postac iloczynową po dzisiejszej lekcji mysle ze
bym juz zrobil
tzn Δ , wspolrzedne wektora i postac iloczynową po dzisiejszej lekcji mysle ze
bym juz zrobil 
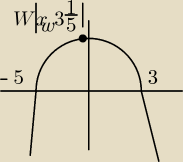
 co nie znaczy ,że ten Twój i Nikki sposób jest błędny ( poprawny jak
najbardziej)
Na maturze czas jest [C{drogocenny]] ,
stąd należy wybierać najkrótszą drogę ( jak w życiu........
Pora
co nie znaczy ,że ten Twój i Nikki sposób jest błędny ( poprawny jak
najbardziej)
Na maturze czas jest [C{drogocenny]] ,
stąd należy wybierać najkrótszą drogę ( jak w życiu........
Pora  Dobrej nocy Godzio
Dobrej nocy Godzio  ... do jutra ....
... do jutra ....

 to była pierwsza myśl... zgadzam się, że czas na maturze jest drogocenny
to była pierwsza myśl... zgadzam się, że czas na maturze jest drogocenny  Aza przy okazji Twojego rozwiązania też się czegoś nauczyłam − zauważyłam, że a<0, ale
brakowało mi trzeciego równania (tego z xw)
Aza przy okazji Twojego rozwiązania też się czegoś nauczyłam − zauważyłam, że a<0, ale
brakowało mi trzeciego równania (tego z xw) 