równanie z wartoscią bezwzględną
kamil: rozwiązać równość
|2x − 3| = |x − 3|
9 lis 21:01
scc: rozwazamy przypadki tylko gdy 2x−3≥0 i x−3≥0
2x−3=x−3
x=0
9 lis 21:18
kamil: przecież równie dobrze 2x−3≤0 i x−3≤0 nie rozumiem
ja to tak liczyłem, i nie wiem czy dobrze
|2x − 3| = |x − 3|
2x − 3 = |x − 3| lub 2x − 3 = −|x − 3|
2x − 3 = |x − 3| lub −(2x − 3) = |x − 3|
|x − 3| = 2x − 3 lub |x − 3| = −(2x − 3)
x − 3 = 2x − 3 lub x − 3 = −(2x − 3) lub x − 3 = −(2x − 3) lub x − 3 = 2x − 3
−x = 0 lub x−3 = −2x +3 lub x−3 = −2x +3 lub −x= 0
x=0 lub 3x = 6 −> x=2 lub 3x = 6 −> x=2 lub x=0
nie wiem czy dobrze to rozwiązuje
9 lis 21:28
kamil: czy ktoś może mi to sprawdzic
12 lis 21:46
Godzio:
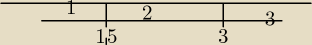
przekombinowane

rozpatrujesz dla 3 przypadków
1) (−∞,1,5)
−2x+3=−x+3
x=0
2) <1,5,3)
2x−3=−x+3
x=2
3)<3,∞)
2x−3=x−3
x=0

12 lis 22:10
kamil: dzięki Godzio
12 lis 22:42
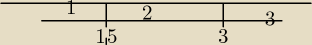 przekombinowane
przekombinowane  rozpatrujesz dla 3 przypadków
1) (−∞,1,5)
−2x+3=−x+3
x=0
2) <1,5,3)
2x−3=−x+3
x=2
3)<3,∞)
2x−3=x−3
x=0
rozpatrujesz dla 3 przypadków
1) (−∞,1,5)
−2x+3=−x+3
x=0
2) <1,5,3)
2x−3=−x+3
x=2
3)<3,∞)
2x−3=x−3
x=0 