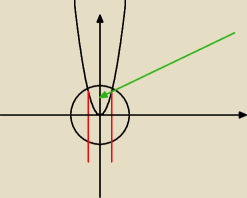
Problem z obliczeniem pola obszaru (całka) Martyna: Problem z obliczeniem pola obszaru (całka) Witam, oto treść zadania: Znaleźć pole obszaru ograniczonego krzywymi x²+y²=2 oraz y=x² Obliczyłam punkty przecięcia obu funkcji: x=1, x=−1, jest to przedział całkowania (oznaczony na czerwono). Więc muszę policzyć obszar zaznaczony zieloną strzałką, tylko nie do końca wiem jak się za to zabrać. Czy jest ktoś w stanie dać mi małą podpowiedź?

MQ: Obszar jest symetryczny więc wystarczy całkować od 0 do 1 f1=√2−x² f2=x² Całkujesz w podanym przedziale całkę: ∫(f1−f2)dx

MQ: Sorry pomyłka −− zmyliła mnie zielona strzałka. Skoro obszar zaznaczony na czerwono, to ∫(f1+f2)dx

Martyna: aha teraz rozumiem, dzięki Ci bardzo A mógłbyś mi jeszcze wytłumaczyć, co w przypadku gdy obszar byłby ograniczony okręgiem x²+y²=2 i parabolą, ale odwróconą, y²=x. Która funkcja jest funkcją ograniczającą z góry, a która z dołu?

daras: ta która jest wyżej ogranicz z góry, a ta która jest niżej z dołu−to tak ja z sufitem i podłogą najlepiej sobie pokoloruj wystarczą 4 kredki