Parametr M
Bartuś: Dla jakich wartości parametru m rozwiązaniem układu: 4x+5y=m−1 i 2x+3y=m+3 jest para liczb o
przeciwnych znakach?
2 wrz 17:42
J:
A jaki poziom ?
2 wrz 17:45
razor: 4x+5y = m−1
4x+6y = 2m+6
odejmując pierwsze od drugiego mamy
y = 2m+6−m+1 = m+7
4x+5m+35=m−1
4x = −4m−36
x = −m−9
y = m+7
I teraz 2 układy równań do rozwiązania: x>0,y<0 lub x<0,y>0
2 wrz 17:48
J:
...albo : x*y < 0 ⇔ −(m+9)(m+7) < 0 ⇔ (m+9)(m+7) > 0 ..
2 wrz 17:52
razor: racja, nie pomyślałem
2 wrz 17:53
Bartuś: Nie rozumiem za bardzo, jak to dwa układy równań? Mam podstawić dowolna liczbę za m?
2 wrz 17:54
J:
Iloczyn: x*y ma być ujemny .... i popatrz na post 17:52
2 wrz 18:05
Bartuś: Po rozpisaniu wyszło mi:
m2 −16m−63<0 ⇔ m2+16m+63>0
Co dalej zrobić?
2 wrz 18:06
J:
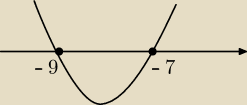
A teraz widzisz ?
2 wrz 18:11
Bartuś: teraz muszę wyliczyć deltę?
2 wrz 18:12
J: Nie... popatrz kiedy ( dla jakiego m ) gałęzie paraboli są nad osią
2 wrz 18:37
Bartuś: dla m∊(−∞,−9> i <−7,∞) ale skąd to −9 i −7?
2 wrz 18:40
J: .. przedziały otwarte.... m+7 = 0 ⇔ m = − 7 ( miejsca zerowe)
2 wrz 18:42
J: .. i oczywiście między przedziałami słowo: lub
2 wrz 18:42
Bartuś: ale nie rozumiem jak to: m2 −16m−63<0 ⇔ m2+16m+63>0 ma się do tego m∊(−∞,−9) lub (−7,∞)
2 wrz 18:44
J:
(m+7)(m+9) ... to postać iloczynowa trójmianu kwadratowego, z której od razu widac miejsca
zerowe
2 wrz 18:49
Bartuś: Czyli to jest rozwiązaniem zadania? m∊(−∞,−9) lub (−7,∞)
Bo już się pogubiłem
2 wrz 18:50
J: Tak ... to jest rozwiązanie.
2 wrz 18:51
Bartuś: Dziękuje bardzo za pomoc
2 wrz 18:56